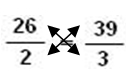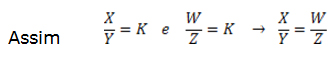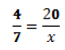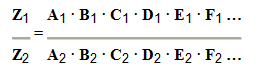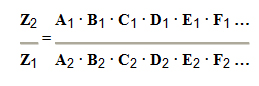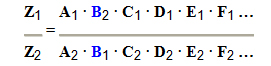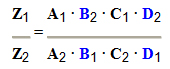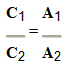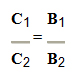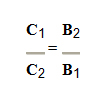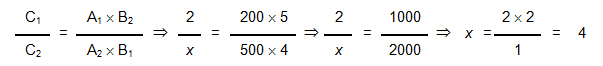Equilibrando Proporções

Grandeza: é toda relação que envolve medidas. O ato de medir é comparar quantitativamente uma grandeza física com uma unidade pré-definida em uma escala. As grandezas devem estar sempre acompanhadas de suas unidades já que é uma relação numérica estabelecida com um objeto. Por exemplo: a temperatura em um determinado local, o volume de um tanque de combustível no automóvel, a massa de um corpo qualquer, a quantidade botões em uma camisa etc. são exemplos de grandezas.

Razão: É a divisão ou relação entre duas grandezas.

Exemplo: Se em duas classes tivermos 40 meninos e 30 meninas, qual a razão entre:

  a) O número de meninos e o número de meninas?

  b) O número de meninas e o número de meninos?

  a) É um caso de Razão direta:

Razão = número de meninos = 40 = 4
              número de meninas = 30 = 3

Portanto, há quatro meninos para três meninas nessa classe.

  b) Também é um caso de Razão direta:

Razão = número de meninas = 30 = 3
              número de meninos = 40 = 4

Proporção: É a igualdade entre as razões.

Exemplo: meu carro faz 13 km/L de combustível, então para 26 km preciso de 2 litros, para 39 km preciso de 3 litros e assim por diante.

1ª situação:                                                                               2ª situação:

R₁ = 26 = 13                                                                           R₂ = 39 = 13
          2       1                                                                                      3       1

portanto, R1 = R2, logo formam uma proporção.

Observe:

•Se você multiplicar em ‘xis’, o resultado será o mesmo:  26 x 3 = 2 x 39 = 78

Numa proporção quando somamos ou subtraímos termo a termo a razão não se altera:

Termo Geral das proporções:

Grandezas Diretamente Proporcionais (G.D.P.)

Duas grandezas são ditas diretamente proporcionais, quando o aumento de uma delas implica no aumento da outra, quando a redução de uma delas implica na redução da outra também, ou seja, a ação em uma delas implicará em uma reação idêntica na outra.

Exemplo1:

Numa receita para fazer pudim, eu uso duas latas de leite condensado, seis ovos e três garrafas de leite para fazer uma porção de pudim.
Se eu quiser fazer duas porções de pudins, vou precisar de quatro latas de leite condensado, doze ovos e seis garrafas de leite, ou seja, o dobro de ingredientes para o dobro de porções.

Exemplo2:

Observe a tabela abaixo que relaciona o preço que tenho que pagar em relação à quantidade de pães que compre:

Preço e quantidade de pães são grandezas diretamente proporcionais. Portanto se compro mais pães, pago mais, se compro menos pães, pago menos. Observe que quando dividimos o preço pela quantidade de pães obtemos sempre o mesmo valor.

Propriedade: Em grandezas diretamente proporcionais, a razão sempre será constante.

Grandezas Inversamente Proporcionais (G.I.P.)

Duas grandezas são ditas inversamente proporcionais quando o aumento da primeira implica na redução da segunda ou quando na redução da primeira implica no aumento da segunda, ou seja, a ação em uma delas implicará em uma reação inversa e de mesma intensidade na outra.

Exemplo: Numa viagem, quanto maior a velocidade média no percurso, menor será o tempo de viagem. Quanto menor for a velocidade média, maior será o tempo de viagem.

Observe a tabela abaixo que relaciona a velocidade média e o tempo de viagem, para uma distância de 600 km.

Velocidade média e Tempo de viagem são grandezas inversamente proporcionais, assim, para uma mesma distância, se viajo mais depressa levo um tempo menor, se viajo com menor velocidade média levo um tempo maior.

Propriedade: Em grandezas inversamente proporcionais, o produto é constante.

60 x 10 = 100 x 6 = 12 x 5 = 150 x 4 = 200 x 3 = 300 x 2 = k (constante)

Regra de três simples direta

Uma regra de três simples direta é uma forma de relacionar grandezas diretamente proporcionais.
Para resolver problemas, tomaremos duas grandezas diretamente proporcionais X e Y e outras duas grandezas W e Z também diretamente proporcionais, de forma que tenham a mesma constante de proporcionalidade K.

Exemplo: Na extremidade de uma mola colocada verticalmente foi pendurado um corpo de 4 kg e verificamos que a mola esticou 20cm. Se colocarmos outro corpo com 7 kg de massa na extremidade dessa mola, quantos centímetros ela esticará?

Sendo x a medida procurada e de acordo com os dados do problema, temos:

As grandezas envolvidas, massa e deslocamento, são diretamente proporcionais. Conhecidos três dos valores no problema nós podemos obter o quarto valor x, e, pelos dados da tabela, podemos montar a proporção:

Regra de três composta

É um processo de relacionamento de grandezas em que pode ocorrer uma das três possibilidades:

1. Todas são diretamente proporcionais;
2. Todas são inversamente proporcionais;
3. Uma mistura das duas situações anteriores.

O método funcional para resolver um problema dessa ordem é montar uma tabela com duas linhas, sendo que a primeira linha indica as grandezas relativas à primeira situação enquanto que a segunda linha indica os valores conhecidos da segunda situação.
Sendo A1, B1, C1, D1, E1, ... os valores associados às grandezas para uma primeira situação e A2, B2, C2, D2, E2, ... os valores associados às grandezas para uma segunda situação, montamos a tabela abaixo, lembrando que estamos interessados em obter o valor numérico para uma das grandezas, por exemplo Z2 se conhecemos o correspondente valor numérico Z1 e todas as medidas das outras grandezas.

1ª Possibilidade: Quando todas as grandezas são diretamente proporcionais à grandeza Z, resolvemos a proporção na mesma seqüência em que elas aparecem:

2ª Possibilidade: Quando todas as grandezas são indiretamente proporcionais à grandeza Z, invertemos a grandeza Z e resolvemos a proporção na mesma seqüência em que elas aparecem:

3ª Possibilidade: Quando todas as grandezas são diretamente proporcionais à grandeza Z, exceto quando uma (ou mais) delas que é inversamente proporcional à grandeza Z (por exemplo, a grandeza B), resolvemos a proporção invertendo a grandeza B1 com a grandeza B2 e mantemos as outras na mesma proporção direta em que aparecem:

Por exemplo, se temos cinco grandezas envolvidas: A, B, C, D e Z, sendo a primeira A e a terceira C diretamente proporcionais à grandeza Z e as outras duas B e D inversamente proporcionais à grandeza Z, montamos a tabela para  resolvermos a proporção:

Fazendo as devidas inversões na proporção:

Exemplos:

1. Funcionando durante 6 dias, 5 máquinas produziram 400 peças de uma mercadoria. Quantas peças dessa mesma mercadoria serão produzidas por 7 máquinas iguais às primeiras, se essas máquinas funcionarem durante 9 dias?

Vamos representar o número de peças pela letra P e de acordo com os dados do problema, vamos organizar a tabela:

Agora a análise deverá ser feita de uma forma independente para cada par de grandezas dadas em relação à grandeza nº de peças (a referência nossa para as outras grandezas).

Consideramos as grandezas número de peças (C) e número de dias (A). Devemos usar a lógica para constatar que se tivermos maior número de dias produziremos maior número de peças e se tivermos menor número de dias produziremos menor número de peças. Assim temos que estas duas grandezas são diretamente proporcionais.

Vamos considerar agora as grandezas número de peças (C) e número de máquinas (B). Usando a lógica novamente para constatar que se tivermos mais máquinas operando produziremos mais peças e se tivermos menos máquinas operando produziremos menos peças. Assim temos que estas duas grandezas também são diretamente proporcionais.

Concluímos que todas as grandezas envolvidas são diretamente proporcionais, portanto basta resolver a proporção na ordem em que aparecem:

Resolvendo a proporção, obtemos  P = 840. Assim, se as sete máquinas funcionarem durante nove dias serão produzidas 840 peças.

2. Um motociclista, rodando 4h por dia, percorre em média 200 km em 2 dias. Em quantos dias esse motociclista irá percorrer 500 km, se rodar 5 h por dia? (h = hora, km = quilômetro).

Vamos representar o número de dias procurado pela letra X. De acordo com os dados do problema, vamos organizar a tabela:

A grandeza número de dias (C) é a que servirá como referência para as outras grandezas (já que um dos valores desta grandeza é desconhecido). Analisaremos se as grandezas Quilômetros (A) e Horas por dia (B) são diretamente proporcionais ou inversamente proporcionais à grandeza C que representa o número de dias. Como já foi comentado anteriormente, esta análise deve ser feita de uma forma independente para cada par de grandezas.

Consideremos as grandezas Número de dias e Quilômetros. Se rodarmos maior número de dias, percorreremos maior quilometragem e se rodarmos menor número de dias percorreremos menor quilometragem. Assim temos que estas duas grandezas são diretamente proporcionais.

Agora para a outra análise, vamos agora considerar as grandezas Número de dias e Horas por dia. Para o mesmo percurso, verificamos que para realizar o mesmo percurso, se tivermos maior número de dias utilizaremos menor número de horas por dia e se tivermos menor número de dias necessitaremos maior número de horas. Logo, estas duas grandezas são inversamente proporcionais (é necessária uma inversão na multiplicação) e desse modo:

Resolvendo esta proporção, obtemos x = 4, significando que para percorrer 500 km, rodando 5 h por dia, o motociclista levará 4 dias.