A diferença das Médias
O que é Média?  Uma média de uma série de números é o valor que pode substituir cada um dos números dados sem alterar a característica entre eles, que pode ser a soma, o produto ou a soma dos inversos.
Média Aritmética Simples
A característica da média aritmética simples é a soma dos números. É o resultado da divisão da soma de n valores por n. A fórmula é a seguinte:

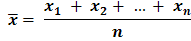
Por exemplo, a média entre 4, 12 e 8 será:

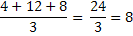
Ou a média entre 3, 36 e 54 é igual a 31, e de fato, ao substituirmos os três números por 31 não alteramos a soma dos três números que é igual a 93:
3 + 36 + 54 = 31 + 31 + 31 = 93

Média Aritmética Ponderada
Neste tipo de média aritmética atribuímos “pesos” aos números envolvidos, mas não mudamos a característica que é a soma deles (multiplicados pelos seus respectivos pesos). Nela cada número que fará parte da média terá um peso. Este peso será multiplicado pelo número, que serão somados e divididos depois pela soma dos pesos.

A fórmula será a seguinte:

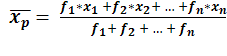
Veja o exemplo:

Média Ponderada:

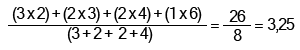
Note que: (2 +2 + 2) + (3 + 3) + (4 + 4) + 6 = (3,25 ´ 3) + (3,25 ´ 2) + (3,25 ´ 2) + 3,25 = 26

 
Média Geométrica Simples
A característica da média geométrica simples é o produto entre os números envolvidos. Entre n valores, é a raiz de índice n do produto desses valores.
A fórmula será a seguinte: 

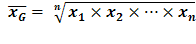
Por exemplo: A média geométrica simples entre os números 3, 36 e 54 é igual a

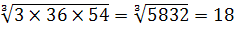
e, de fato, ao substituirmos os três números por 18, não alteramos o produto entre os três números 

(18 X 18 X 18) que é igual a 5832.

Média Harmônica Simples
A média harmônica é o inverso (normalmente chamado de recíproco) da média aritmética dos inversos (recíprocos) dos números dados. Em outras palavras: a média harmônica equivale ao inverso da média aritmética dos inversos de n valores.
Parece complicado, mas é bastante simples. A característica da média harmônica é a soma dos inversos dos números. A fórmula é a seguinte:

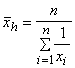
Veja o exemplo: Média harmônica entre 2, 6 e 8. Uma forma prática: primeiramente é necessário calcular a média aritmética dos inversos dos valores dados:

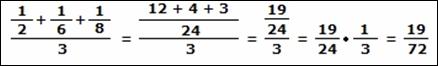
Agora calculamos o inverso do resultado encontrado:

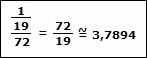
Podemos ter também casos em que a média harmônica será ponderada. Nestes casos utilizamos a seguinte fórmula:

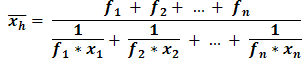
Em todas as médias o resultado sempre estará entre o maior e o menor número dado.
Para os mesmos valores, a média aritmética terá o maior valor, seguida da média geométrica e depois a média harmônica.

Referências:
LIMA et al : A Matemática do Ensino Médio. Volume 2 Rio de Janeiro: SBM, 1998