Caro estudante, este é um tutorial de ajuda sobre o tema: Probabilidade. Através da leitura deste tutorial e da discussão do tema com seus colegas e professor acreditamos que você poderá compreender o conceito da Probabilidade. A simulação Probabilidade Roxa, trata questões com enfoque em um tipo de probabilidade: a probabilidade condicional, mas, para um melhor entendimento da matéria, abordamos
explicações que englobam a matéria desde o início. Esperamos que este texto possa auxiliá-lo no entendimento do cálculo das probabilidades.

1. O que é Probabilidade?

Experiências que são repetidas sob as mesmas condições e que produzem resultados diferentes são chamadas de aleatórias. Como por exemplo: lançar uma moeda, lançar um dado, retirar uma carta de um baralho, sortear um número. Em experiências aleatórias não temos como garantir o resultado que será encontrado, mas podemos calcular as chances de um determinado resultado ocorrer, ou seja, calcular a probabilidade de certo resultado (que chamaremos de evento) ocorrer.

Podemos definir a probabilidade como as chances de um resultado ocorrer entre todos os demais que podem acontecer. Esses resultados são chamados de EVENTO e todos os eventos que podem ocorrer são chamados de ESPAÇO AMOSTRAL.

Vamos às definições:

2. Espaço Amostral

Definimos por Espaço Amostral o conjunto de todos os resultados possíveis de um experimento aleatório, geralmente esse conjunto é indicado por U ou S
Utilizaremos neste texto a letra S para definir o Espaço Amostral.

Exemplos:

1) Jogar um dado e observar o número da face que ficar para cima, o espaço amostral desse experimento aleatório seriam todas as possibilidades, ou seja:

S={1,2,3,4,5,6} e o número de possibilidades seria 6, ou seja; n(S)=6

2) Sortear uma bola em uma urna que contém 100 bolas numeradas de 1 à 100.

S = {1,2,3,4,...,100} e o número de possibilidades seria 1000, ou seja: n(s) = 100

3. Evento

Um Evento pode ser definido como a ocorrência ou resultado desejado entre todos os possíveis. Dessa forma, definimos como evento qualquer subconjunto de um Espaço Amostral S.

Exemplos:
1) O Evento “lançar um dado e observar a face voltada para cima e estar ser um número par” é o subconjunto E {2,4,6} de todos os resultados possíveis S {1,2,3,4,5,6}

Assim, E = {2,4,6} e o número de possibilidades de E é igual a 3, ou seja n(E) = 3 .

2) O Evento “ lançar uma moeda e observar a face voltada para cima e esta ser Coroa” é o subconjunto E {coroa} de todos os resultados possíveis S {cara, coroa}

Assim, E = {coroa} e o número de possibilidades de E é igual a 1, ou seja, n(E) = 1.

4. Probabilidade de um Evento ocorrer

Podemos definir a probabilidade P(E) de um evento equiprovável ocorrer é dada pela razão (divisão) entre o número de elementos dos eventos desejados (subconjunto do espaço amostral) pelo número total de eventos possíveis (espaço amostral)

P(E) = ________Número de elementos dos evento desejado________   ou seja : P(E) = N(E)
                 Número de elementos de todos os resultados possíveis                                    N(S)

Exemplo:

Vamos calcular a seguinte probabilidade: Considere o lançamento de um dado honesto (ou seja, todos os resultados são igualmente possíveis) , ao lançar o dado e observarmos a face voltada para cima, qual será a probabilidade da face ser igual ao número 5?

Temos então:
Espaço Amostral S = {1,2,3,4,5,6,}, ou seja, n(S) = 6
Evento “ face ser igual à 5” , E {5}, ou seja, n (E) = 1

Então a Probabilidade deste evento ocorrer é :

P(E) = n(E) = 1 = 0,16666666.... = 16,66% ou 16,67%
           n(S) = 6

5. Probabilidade da União de Dois Eventos

Tratamos como união de dois eventos quando são eventos que podem ocorrer em um mesmo espaço amostral, ou seja, levamos em consideração o resultado de um ou o resultado do outro.

Assim, e A e B são eventos em um mesmo espaço amostral S,  então A união com B, ou seja A U B é o evento que ocorre se, e somente se, ocorre o Evento A ou ocorre o Evento B.

Calculamos essa probabilidade somando a probabilidade dos dois eventos, mas subtraindo a probabilidade de eventos que podem ser comum aos dois eventos.

Da seguinte forma:

Ou seja: é a soma das probabilidades dos dois eventos, porém subtraindo aquilo que é comum aos dois eventos (para que não seja somado em duplicidade)

Exemplo:

Vamos considerar novamente o lançamento de um dado honesto, e os seguintes eventos: E1 = “ser par”  e  E1 = “ sem divisor de 6”
Ou seja:           E1 = {2,4,6}       n(E1) = 3
                         E2 = {1,3,6}       n(E2) = 3

Não podemos simplesmente somar as duas Probabilidades, pois se olharmos mais detalhadamente verificaremos que o número 6 aparece tanto no Evento E1 (ser par) como no Evento E2 (divisor de 6) , assim, estaremos contando duas vezes um mesmo elemento, por isso a necessidade de diminuir o elemento que é comum aos dois eventos.

Dessa forma, temos então que a Probabilidade de “ser par” ou “ ser divisor de 6” é dada por:

P(E1 U P2) = P(E1) + P(E2) - P (E1 ∩ E2)

P(E1 U P2) = 3/6 + 3/6 - 1/6 = 5/6 = 5/6 = 0,8333333... = 83,33%

6. Probabilidade de Eventos Simultâneos (ou sucessivos)

Considere A e B dois eventos em um mesmo espaço amostral, eles são ditos independentes quando a realização de um, não afeta a probabilidade do outro e vice-versa, e são ditos simultânenos ou sucessivos quando ocorre se, e somente se, o Evento A e ocorre o Evento B.

Para eventos independentes, calculamos a probabilidade destes eventos através do teorema da multiplicação que é dado por:

P(A ∩ B) = P(A) . P(B)  

Ou seja, a Probabilidade do evento A ocorrer e o evento B ocorrer, será dada pela multiplicação entre as probabilidades.

Exemplo 1:
Considere dois lançamentos sucessivos de um dado honesto, qual a probabilidade de que o resultado do primeiro lançamento seja 2 e no segundo seja um número maior que 4?

Vamos inicialmente ao cálculo da probabilidade de cada um dos eventos.
Sabemos que para cada um dos eventos, o espaço amostral é o mesmo, S = {1,2,3,4,5,6} e n(S) = 6.

Vamos aos eventos:

E1 = “ ser 2” , então E1 = {2} e temos que n(E1) = 1
E2 = “ ser maior que 4” , então E2 = {5,6} e temos que n(E2) = 2

P(E1 ∩ E2) = P(E1) . P(E2)

P(E1 ∩ E2) = 1/6 . 2/6 = 2/36 = 1/18 = 0,05555555... = 5,55%

Para eventos em que um pode interferir no resultado do outro (ou seja, eventos dependentes) precisamos de uma análise mais detalhada.

Exemplo 2:

Uma rifa contém 20 números e serão realizados dois sorteios sucessivos. Eu possuo 4 números dessa rifa, qual a probabilidade de eu ser premiado tanto no primeiro quando no segundo sorteio?

Vamos a analise:
Espaço Amostral S = {20 números da rifa} n (S) = {20}
Evento 1 {ser sorteado com um dos 4 números que possuo}
Evento 2 {ser sorteado com um dos 3 números que possuo}

O detalhe que temos que considerar nesta questão é que se eu for premiado com um número no primeiro sorteio, eu tive 4 chances em 20 , e para ser premiado novamente em um segundo sorteio, eu terei 3 chances em 19 (pois já saiu um número no sorteio anterior)

Assim a probabilidade será dada por:

P(E1 ∩ E2) = P(E1) . P(E2)

P(E1 ∩ E2) = 4/20 . 3/19 = 12 / 380 = 3/95 = 0,0315789 = 3,16%

Agora, vejamos o cálculo de algumas probabilidades:

Probabilidade (A)  “ escolhermos ao acaso, nesta turma, uma menina”
Como temos no total 16 alunas, então n(A) = 16
Temos como espaço amostral a quantidade de alunos e alunas, então  n(S) = 30

Então a Probabilidade deste evento ocorrer é:

P(A)=n(A) = 16 =08 = 0,53333 ... ≅ 53,33%
         n(S)    30   15   

Vejamos agora outro exemplo: A probabilidade de praticar vôlei, sabendo que é uma menina?    Ou seja: B (vôlei | menina)

Podemos resolver esse problema, reduzindo o espaço amostral a partir da informação parcial, neste caso, como sabemos que se trata de uma menina, temos 16 opções, e para calcular a probabilidade de praticar vôlei, temos:

P(volei | menina) = n(B) = 10 =  5 =  0,625 = 62,50%
                               n(S)    16     8

Mas de uma forma geral, podemos determinar a probabilidade de um evento ocorrer sabendo da ocorrência de um evento anterior por:

p(A\B) = P(A ∩ B)
                p(B)   

Então, para resolver a mesma questão acima temos:

p(volei | menina) = P(volei e menina)
                                     P(menina)  

             10
P(A\B)= 30 = 10 = 5 = 0,625 = 62,50%
             16 = 16 = 8
             30

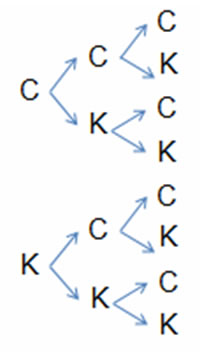
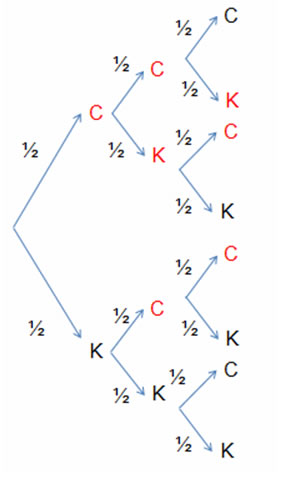
6. Probabilidade de Eventos Simultâneos (ou sucessivos)

Considere A e B dois eventos em um mesmo espaço amostral, eles são ditos independentes quando a realização de um, não afeta a probabilidade do outro e vice-versa, e são ditos simultânenos ou sucessivos quando ocorre se, e somente se, o Evento A e ocorre o Evento B.

Para eventos independentes, calculamos a probabilidade destes eventos através do teorema da multiplicação que é dado por:

P(A ∩ B) = P(A) . P(B)  

Ou seja, a Probabilidade do evento A ocorrer e o evento B ocorrer, será dada pela multiplicação entre as probabilidades.

Exemplo 1:
Considere dois lançamentos sucessivos de um dado honesto, qual a probabilidade de que o resultado do primeiro lançamento seja 2 e no segundo seja um número maior que 4?

Vamos inicialmente ao cálculo da probabilidade de cada um dos eventos.
Sabemos que para cada um dos eventos, o espaço amostral é o mesmo, S = {1,2,3,4,5,6} e n(S) = 6.

Vamos aos eventos:

E1 = “ ser 2” , então E1 = {2} e temos que n(E1) = 1
E2 = “ ser maior que 4” , então E2 = {5,6} e temos que n(E2) = 2

P(E1 ∩ E2) = P(E1) . P(E2)

P(E1 ∩ E2) = 1/6 . 2/6 = 2/36 = 1/18 = 0,05555555... = 5,55%

Para eventos em que um pode interferir no resultado do outro (ou seja, eventos dependentes) precisamos de uma análise mais detalhada.

Exemplo 2:

Uma rifa contém 20 números e serão realizados dois sorteios sucessivos. Eu possuo 4 números dessa rifa, qual a probabilidade de eu ser premiado tanto no primeiro quando no segundo sorteio?

Vamos a analise:
Espaço Amostral S = {20 números da rifa} n (S) = {20}
Evento 1 {ser sorteado com um dos 4 números que possuo}
Evento 2 {ser sorteado com um dos 3 números que possuo}

O detalhe que temos que considerar nesta questão é que se eu for premiado com um número no primeiro sorteio, eu tive 4 chances em 20 , e para ser premiado novamente em um segundo sorteio, eu terei 3 chances em 19 (pois já saiu um número no sorteio anterior)

Assim a probabilidade será dada por:

P(E1 ∩ E2) = P(E1) . P(E2)

P(E1 ∩ E2) = 4/20 . 3/19 = 12 / 380 ≅ 3/95 = 0,0315789 ≅ 3,16%

Também podemos utilizar a expressão

P(E1 ∩ E2) = P(E1|E2) . P(E2) ou seja, E2|E1 que dizer, E2 ocorrer, sabendo que E1 já ocorreu, que nos leva ao mesmo raciocínio exposto acima.

Exemplo 3:

Dependendo da questão, quando o que nos interessa é uma combinação de resultados podemos construir um diagrama de árvore para o experimento e associar probabilidade a cada um de seus galhos.

Vamos a um exemplo: Ao lançarmos uma moeda três vezes, qual a probabilidade de obtermos exatamente duas coroas?

Vamos ao diagrama (no qual C= Coroa e K = Cara)

Podemos calcular essa probabilidade de duas formas:

1) Através do diagrama, verificamos que são 8 resultados diferentes para os três lançamentos.

Assim P(K) = 3/8 = 0,375 = 37,5%

2) Analisarmos como dois eventos sucessivos e dependentes, pois o segundo evento depende da ocorrência do segundo.

P(E) = (1/2 . 1/2 . 1/2) ou (1/2 . 1/2 . 1/2) ou (1/2 . 1/2 . 1/2) Mas o termo ou significa uma ou outra probabilidade o que resulta na união dos eventos, assim: P(E) = 1/8 + 1/8 + 1/8 = 3/8

Caro(a) estudante, esperamos poder ajudá-lo no entendimento do tópico de Probabilidade. A probabilidade merece destaque, pois está ligada diretamente a vários fatos de nossa vida real como a previsão do tempo, a probabilidade aplicada a genética, em química, jogos e outros.

Para saber mais sobre o assunto, deixamos aqui algumas sugestões de outros objetos de aprendizagem e de alguns textos interessantes sobre o assunto, converse com seu professor(a) e explore o tema, temos certeza de que será muito interessante.

REFERÊNCIAS BIBLIOGRÁFICAS

IEZZI , Gelson et al – Matemática: ciências e aplicações - Volume 2 – São Paulo: Atual, 2004.
LIMA, Elon et al – A Matemática do Ensino Médio – Volume 2 – Rio de Janeiro: SBM, 1998.