T E O R I A     (Referencial Físico Matemático) Imprimir

1. CAMPO ELÉTRICO UNIFORME

Define-se como campo elétrico uniforme uma região do espaço onde o vetor campo elétrico possui, em todos os pontos, a mesma direção, o mesmo sentido e o mesmo módulo. Idealmente, o campo elétrico uniforme seria produzido por uma distribuição plana, infinita e uniforme de cargas elétricas, como mostra a figura 1.

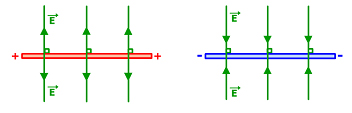
Figura 1 - Campo elétrico produzido por uma distribuição plana, infinita e uniforme de cargas.

Na prática, este campo pode ser obtido na região interna de duas placas metálicas planas e de mesma área, paralelas e eletrizadas com cargas de sinais opostos. Repare na figura 2: isso é válido apenas no interior das placas, pois nas extremidades da placa, o campo elétrico não é uniforme.

Quando a distância de separação das placas é muito menor que as dimensões da placa, a quantidade de carga na superfície externa é muito pequena e o efeito nas bordas é desprezível. Nesse caso, assume-se que o campo elétrico produzido no interior das placas é uniforme.

1.1 Análise geométrica do campo elétrico uniforme

Como o vetor campo elétrico tem sempre a mesma direção, as linhas de força tornam-se retilíneas. E o fato de vetor campo elétrico apresentar a mesma intensidade em todos os pontos faz com que as linhas de força sejam igualmente espaçadas. (Figura 2).

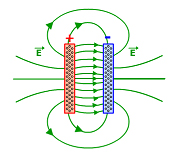
Figura 2 - Campo elétrico produzido por duas placas metálicas planas e de mesma área, paralelas e eletrizadas com cargas de sinais opostos.

Lembre-se que a intensidade do campo elétrico é proporcional à densidade das linhas de força, ou seja, quanto mais intenso seja o campo, mais próximas as linhas estarão. Portanto, para indicar sempre a mesma intensidade para o campo elétrico, elas devem possuir sempre a mesma distância entre si.

As superfícies equipotenciais na região de campo elétrico uniforme são planos paralelos entre si (veja figura 3), cujo valor do potencial elétrico vai diminuindo à medida que se caminha no sentido da linha de força. Elas devem ser sempre perpendiculares às linhas de força.

Figura 3 - Representação das superfícies equipotenciais em uma região de campo elétrico uniforme.

1.2 Trabalho da força elétrica num campo elétrico uniforme

Observando a figura 4, considere um campo elétrico uniforme e uma partícula eletrizada que se desloque em seu interior de um ponto A a um ponto B.

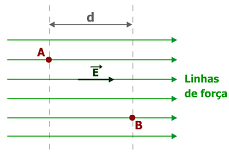
Figura 4 - Efeito do campo elétrico sobre uma partícula eletrizada que se desloca de A até B.

Sobre a partícula estará atuando uma força elétrica constante, visto que o campo é uniforme, temos: F= q . E           (1)

Partindo da definição de trabalho realizado por uma força constante e paralela à direção do movimento, temos:

t_AB = F . d          (2)

Substituindo F

t_AB = q . E . d          (3)

Repare que d não corresponde à distância entre os pontos A e B. Sendo d é a distância entre a superfície equipotencial que passa pelo ponto A e a superfície equipotencial que passa por B.

1.3 Diferença de potencial num campo elétrico uniforme


A definição geral de trabalho realizado pelo campo elétrico sobre uma carga que se desloca desde A a B, devido a uma diferença de potencial U_AB, é:

t_AB = q . U_AB           (4)

Considerando a expressão achada antes para o trabalho realizado pela força elétrica em um campo elétrico uniforme:

t _AB = q . E . d          (5)

E comparando ambas as expressões, concluímos que a diferença de potencial entre A e B é dada por:

U_AB = E . d          (6)

Essa equação obtida para a diferença de potencial elétrico permite a introdução da unidade oficial no SI para a intensidade do campo elétrico. De acordo com a equação anterior, tem-se que:

E = U_AB / d          (7)

Ou seja, a unidade de campo elétrico é designada por [V/m], que é equivalente ao [N/C] utilizado anteriormente.

REFERÊNCIAS