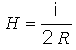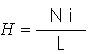|
1.
UM BREVE HISTÓRICO
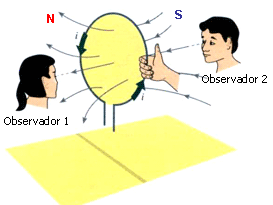
No século XIX, o período compreendido entre os anos de 1819 e 1831 foi dos mais férteis em descobertas no campo da eletricidade. Os fenômenos básicos do eletromagnetismo foram descobertos entre aquelas datas. A observação que Oersted (foto) fez, em 1819, de que uma corrente elétrica desvia a agulha de uma bússola, marca o início de uma época da Física que iria influir profundamente na história da humanidade. A ação mútua de um ímã e uma corrente elétrica aguçaram a curiosidade de muitos investigadores que, até então, não se dedicavam ao estudo da eletricidade, principalmente um grupo de franceses. A primeira grande aplicação da descoberta de Oersted foi feita três anos mais tarde, por Dominique François Arago e Joseph Luis Gay-Lussac. Este, muito conhecido por seus trabalhos em Química. Eles observaram que quando passava corrente em um condutor enrolado numa barra de ferro, esta se imantava: estava, pois, inventado o eletroímã. No mesmo ano, André Marie Ampère estabeleceu a "regra do observador", e descobriu que um solenóide atua como um ímã. Posteriormente, Jean Baptiste Biot e Felix Savart descobriram, ao mesmo tempo, e independentemente um do outro, a lei que leva seus nomes. |
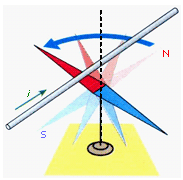
| 2. O EXPERIMENTO DE OERSTED Até o início do século XIX acreditava-se que não existia relação entre os fenômenos elétricos e magnéticos. Em 1819, o professor e físico dinamarquês chamado Hans Christian Oersted observou que uma corrente elétrica era capaz de alterar a direção de uma agulha magnética de uma bússola, como mostra a figura 2.1. |
|
|
(Fonte: http://br.geocities.com/saladefisica10/experimentos/e96.htm) |
|
|
|
|
|
Quando
havia corrente elétrica no fio, Oersted verificou que a agulha
magnética movia-se, orientando-se numa direção
perpendicular ao fio, evidenciando a presença de um campo
magnético produzido pela corrente, como mostra a figura 2.1.
Este campo originava uma força magnética capaz de
mudar a orientação da bússola. Interrompendo-se
a corrente, a agulha retornava a sua posição inicial,
ao longo da direção norte-sul. Observou-se, então,
a existência de uma relação entre a Eletricidade
e o Magnetismo. Ao campo magnético de origem elétrica
chamamos de Campo Eletromagnético.
Conclusão de Oersted:
Surge, a partir daí, o estudo do Eletromagnetismo, que é a parte da Eletricidade que estuda certos fenômenos nos quais intervêm correntes elétricas e campo magnético. Podemos chamar esses fenômenos de eletromagnéticos. Em decorrência dessas descobertas, foi possível estabelecer o princípio básico de todos os fenômenos eletromagnéticos: |
|
|
| 3. CÁLCULO DA INDUÇÃO MAGNÉTICA - LEI DE BIOT-SAVART Chamamos
lei elementar uma lei que relaciona uma variação infinitamente
pequena da variável independente (ou das variáveis
independentes), com uma variação infinitamente pequena
da função (ou das funções). Suponhamos
um condutor AB, percorrido por corrente elétrica de intensidade
i, como mostra a figura 3.1. Essa corrente elétrica produz
um campo magnético. Para calcularmos o vetor B,
em um ponto M qualquer, imaginamos o condutor AB dividido em um
número muito grande de partes: essas partes terão
comprimentos muito pequenos. Calculamos a indução
magnética DB
que cada uma dessas partes produz em M. Depois, efetuamos a soma
vetorial de todos esses campos DB
e obtemos o campo DB
total que o condutor inteiro AB produz em M. A lei que
permite o cálculo do campo DB
(pequeno) produzido por um elemento CD (pequeno) do condutor é
uma lei elementar: é a chamada lei de Biot-Savart. |
||||||
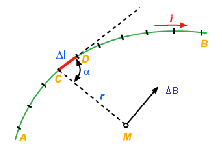 Figura 3.1: Seção AB de um condutor percorrido por uma corrente i. |
||||||
Suponhamos um elemento qualquer do condutor, por exemplo CD, de comprimento Dl. Seja r a distância do ponto M a Dl, a o ângulo formado por Dl e r (fig. 3.1). A lei de Biot-Savart diz que: a indução magnética que o elemento de comprimento Dl produz no ponto M: |
||||||
|
||||||
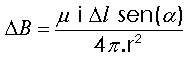 |
||||||
Onde: |
||||||
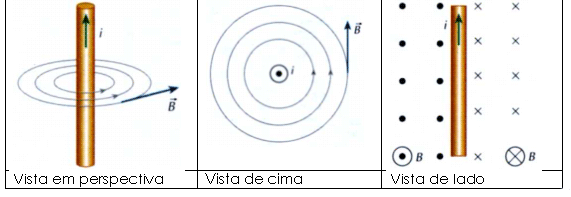
| 4. EXEMPLOS DE CAMPOS MAGNÉTICOS CRIADOS POR CORRENTES ELÉTRICAS 4.1 Indução magnética em um condutor reto |
||||||
|
||||||
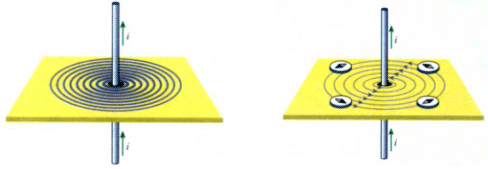
Figura 4.1: a) Linhas de indução geradas por um fio reto percorrido por uma corrente i. b) Sentido das linhas de indução. |
||||||
a) Sentido das Linhas de indução magnética |
||||||
|
||||||
|
|
||||||
|
b) Linhas de Indução
- Condutor Retilíneo
A figura 4.3 ilustra a notação utilizada para a determinação da direção e sentido das linhas de indução magnética.
|
||||||
|
||||||
|
||||||
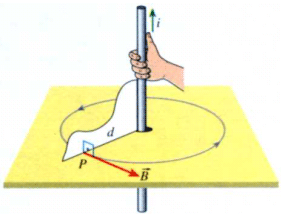 Figura 4.4: Parâmetros para o cálculo da intensidade da indução magnética. |
||||||
onde:
B = Indução magnética num ponto p [T, Tesla]; d = distância entre o centro do condutor e o ponto p considerado [m]; a = intensidade de corrente no condutor [A]. Permeabilidade Magnética do Vácuo: Esta equação é válida
para condutores longos, ou seja, quando a distância r for
bem menor que o comprimento do condutor (d<< |
||||||
4.2 Indução magnética em uma espira circular |
||||||
|
||||||
 Figura 4.5: Indução magnética gerada por uma espira circular e visualização das linhas de indução obtidas experimentalmente com limalha de ferro. |
||||||
a) Intensidade da indução magnética A intensidade da indução magnética devido a uma espira circular de raio R percorrida por uma corrente i, como mostra a figura 4.6, é dada pela Lei de Biot-Savart por: |
||||||
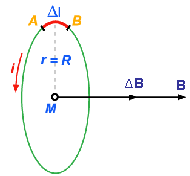 Figura 4.6: Parâmetros para o cálculo da intensidade da indução magnética gerada por uma espira circular de raio R percorrida por uma corrente i. |
||||||
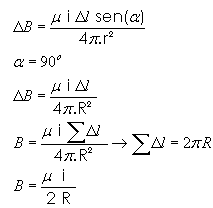 |
||||||
I = corrente pela espira em metros R = raio da espira em metros a = o ângulo formado por Dl e r Permeabilidade Magnética do Vácuo: |
||||||
|
||||||
|
||||||
|
||||||
 |
||||||
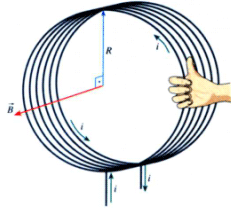
a) Intensidade do vetor B A intensidade do vetor B no centro da bobina vale: |
||||||
Onde N é o número de espiras. |
||||||
4.4 Indução magnética em um selenóide O solenóide (figura 4.9) é um dispositivo em que um fio condutor é enrolado em forma de espiras não justapostas. |
||||||
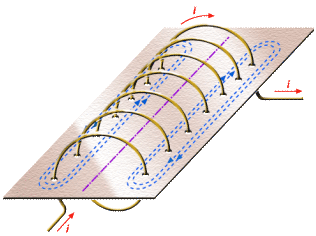 Figura 4.9: Solenóide percorrido por uma corrente i.(Fonte: http://efisica.if.usp.br/eletricidade/basico/campo_corrente/) |
||||||
O campo magnético produzido próximo ao centro do solenóide (ou bobina longa), ao ser percorrido por uma corrente elétrica i, é praticamente uniforme (intensidade, direção e sentido constantes). |
||||||
a) Linhas de indução em um selenóide A direção e sentido das linhas de campo geradas por um solenóide percorrido por uma corrente i são mostrados na figura 4.10. |
||||||
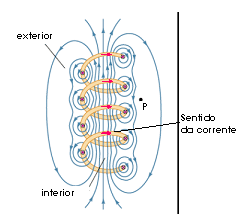 Figura 4.10: Indução magnética gerada no interior e exterior do solenóide. |
||||||
b) Pólos de um solenóide O solenóide se comporta como um ímã, no qual o polo sul é o lado por onde "entram" as linhas de indução, enquanto o lado norte é por onde "saem" as linhas de indução (veja figura 4.11). |
||||||
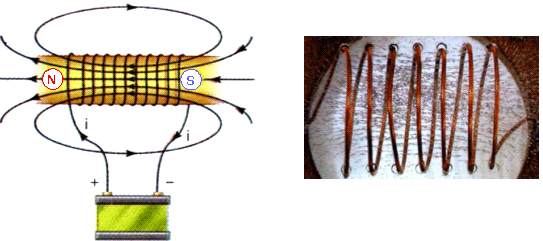 Figura 4.11: Polos gerados por um solenóide percorrido por uma corrente i e linhas de indução obtidas com limalha de ferro (Fonte: Giancoli). |
||||||
Assim, se aproximarmos um ímã do solenóide, o polo sul do imã será atraído pelo polo norte gerado no solenóide indicado pelo sentido do vetor indução magnética B. c) Direção e sentido do vetor B no interior do solenóide
|
||||||
 Figura 4.12: Regra da mão direita para determinar a direção e sentido da indução magnética gerada por um solenóide (Fonte: Giancoli) |
||||||
d) Intensidade do vetor B no interior do solenóide A intensidade do vetor indução magnética
uniforme ao longo de um comprimento L no interior de um solenóide
é dada por (veja figura 4.13): |
||||||
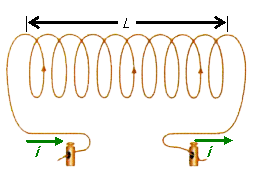 Figura 4.13: Parâmetros para a determinação da intensidade da indução magnética gerada por um solenóide. |
||||||
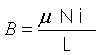 |
||||||
Onde: B = é a indução magnética no centro do solenóide [T, Tesla]; N = número de espiras do solenóide; l = é a intensidade de corrente elétrica que percorre o solenóide [A]; L = comprimento longitudinal do solenóide [m]. 4.5 Indução magnética em um toróide Uma bobina toroidal (ou simplesmente, toróide) é um solenóide em forma de anel, como mostra a figura 4.14. Seu núcleo pode ser de ar ou de material ferromagnético. Geralmente, as bobinas toroidais são feitas com núcleos de ferrite. |
||||||
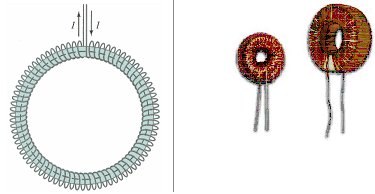 Figura 4.14: Aspecto de um toróide (Fonte: Giancoli). |
||||||
Os toróides são o tipo de bobina capaz de proporcionar a maior concentração das linhas de campo magnético no seu núcleo, que é um caminho fechado para as linhas. Pode ser provado matematicamente que a densidade de campo magnético no interior das espiras (no núcleo) do toróide é dada por: |
||||||
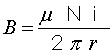 |
||||||
Onde:
B - é a inducão magnética no interior do núcleo do toróide [T]; N - número de espiras da bobina toroidal; I - intensidade de corrente no condutor da bobina, [A]; r - raio médio do toróide [m]. Observação: o raio médio do toróide
é o raio da circunferência no centro do núcleo
do toróide, como mostra a figura 4.15. Não confundir
com o raio externo ou interno e nem com o raio das espiras. |
||||||
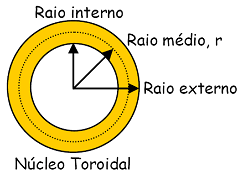 Figura 4.15: Identificação do raio médio de um toróide. |
||||||
Também
pode ser demonstrado matematicamente [Giancoli] que a indução
magnética fora do núcleo de um toróide ideal,
tanto na região externa como interna, é NULO, pois
como o núcleo tem forma circular, ele é capaz de produzir
um caminho magnético enlaçando todas as linhas de
campo.
5. VETOR CAMPO MAGNÉTICO
INDUTOR - FORÇA MAGNETIZANTE
Se, para um toróide, mantivermos a corrente
constante e mudarmos o material do núcleo (permeabilidade
do meio), a indução magnética no interior da
bobina será alterada em função da permeabilidade
magnética do meio. Chamamos de Vetor Campo Magnético
Indutor ou Vetor Força Magnetizante (H)
o campo magnético gerado pela corrente elétrica na
bobina, independentemente da permeabilidade magnética do
material do núcleo (meio). |
||||||
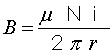 |
||||||
Logo: |
||||||
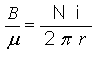 |
||||||
definindo: |
||||||
O módulo do vetor campo magnético indutor ou vetor força magnetizante H num toróide é dado por: |
||||||
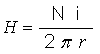 |
||||||
O Vetor Campo Magnético H tem as mesmas características de orientação do vetor indução magnética B, porém independe do tipo de material do núcleo do toróide. A unidade do Vetor Campo Magnético Indutor é Ampère por metro, A/m. Podemos, portanto, concluir que os vetores indução magnética B e campo magnético indutor H se relacionam pela equação: |
||||||
Isso significa que um toróide percorrido uma dada corrente produz uma Força Magnetizante ou Campo Magnético Indutor. Se variarmos o valor da permeabilidade magnética do meio (alterando o material do núcleo do toróide, por exemplo), a indução magnética varia para esta mesma bobina. Quanto maior a permeabilidade magnética Analogamente, podemos determinar a Força Magnetizante H produzida por um condutor retilíneo, para uma espira circular e para um solenóide: |
||||||
|
||||||
Devemos
ter em mente que a permeabilidade magnética de um material
ferromagnético não é constante. É uma
relação entre a Força Magnetizante e a indução
magnética resultante. Essa relação é
dada por: |
||||||
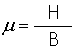 |
||||||
6. O ELETROÍMÃ
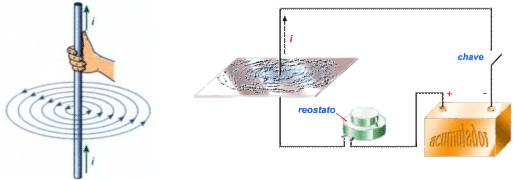
Os eletroímãs são constituídos por uma barra de ferro, ao redor da qual é enrolado um condutor. Quando passa corrente pelo condutor, ela produz um campo magnético; e a barra de ferro, ficando em um campo magnético, se imanta. Em virtude da imantação do pedaço de ferro, o campo magnético resultante assim obtido é muito maior do que o campo criado apenas pela corrente que passa pela bobina (figura 6.1). O uso de eletroímãs oferece várias vantagens: 1a) se quisermos inverter os polos, basta invertermos o sentido da corrente; 2a) é somente a imantação
por corrente elétrica que nos fornece ímãs
muito possantes;
Figura 6.1: Princípio de funcionamento de um eletroímã e guindaste de metais utilizando um eletroímã. |
||||||
Os eletroímãs têm inúmeras aplicações, desde em instalações delicadas, como telégrafos, telefones, disjuntores, relés e campainhas, até em grandes instalações industriais, como em guindastes, mostrado na figura 6.1. Consulte a referência: |
 ).
).