CONDIGITAL

T E O R I A (Referencial Físico Matemático)

1. O NÚCLEO ATÔMICO

Com a configuração da estrutura eletrônica definida, a descoberta do núcleo e de sua estrutura, completa-se um novo modelo atômico (veja a figura 1).

Figura 1 - Estrutura atômica e nuclear. Uma unidade conveniente para medir distâncias subatômicas é o fentômetro (=10^-15m). Esta unidade também é chamada de fermi; 1 fermi=1fm = 10^-15m.
Fonte: SPRACE.

Todo átomo contém em seu centro um núcleo com carga positiva, o qual é muito menor do que o tamanho global do átomo, mas contém a maior parte de sua massa total. Ou seja, a matéria do núcleo é altamente concentrada. A sua densidade é cerca de 2,4. 10¹⁷ kg/m³: a massa de 1 cm³ de um material com esta densidade seria de 240 milhões de toneladas. Os nucleons (nome genérico dado aos prótons e nêutrons contidos no núcleo) são, por sua vez, compostos por quarks, que possuem uma fração da carga do elétron (note que nêutrons são compostos por quarks que resultam em uma carga total nula), e são aqueles entes com nomes “bonitinhos” mostrados na figura 1.

Como os elétrons, os nucleons também têm spin e, portanto, um magnetismo intrínseco com importantes aplicações tecnológicas, como a ressonância magnética nuclear.

1.1 Propriedades dos núcleos

Número Atômico (Z) – número de prótons do núcleo.

Número de Nêutrons (N) – número de nêutrons do núcleo.

Número de Massa (A) – soma do número de prótons e nêutrons: A = Z + N

Isótopos – Os isótopos de um elemento têm o mesmo valor Z, mas diferentes números de N e A. Como exemplos de isótopos do hidrogênio

(A=1, Z=1), temos os deutério (

), que é igual ao átomo de hidrogênio acrescido de um nêutron, logo Z=1 e A=N+Z=1+1=2. Outro isótopo do hidrogênio é o trítio (

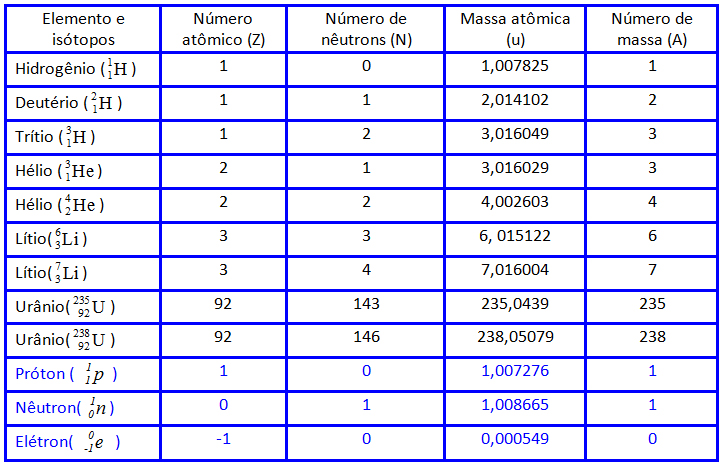
Um nuclídeo é um determinado núcleo com valores definidos para Z e N. Na tabela 1, apresentamos uma lista contendo os valores de A, Z e N de alguns nuclídeos.

Tabela 1 - Massas atômicas dos átomos neutros (inclui a massa dos elétrons) de alguns nuclídeos comuns em processos de fissão e fusão nuclear. Também inclui as dos prótons, nêutrons e elétrons.

Onde u é a unidade de massa atômica, unidade prática de massa utilizada no nível atômico. É, por definição, igual a 1/12 da massa do átomo de carbono-12, cujo valor é:

Nas reações que envolvem núcleos, as transformações de massa em energia, e vice-versa, estão sempre presentes. Nestas reações, é de uso fundamental a equação de Einstein (E=mc²).

Assim, para convertemos massa em energia, basta multiplicar a massa (m) pela velocidade da luz () elevada ao quadrado. Convertendo em energia, temos:

Logo, utilizando a relação E = mc², verificamos que 1u em repouso corresponde a uma energia de ~ 931,5 MeV.

2. A ENERGIA NUCLEAR

A grande proximidade entre os nucleons implica a existência de uma força de interação nuclear atrativa muito intensa para superar a repulsão eletrostática entre os prótons, o que leva a consequências extraordinárias. Uma delas é a possibilidade de obtenção de uma energia cuja origem está no núcleo do átomo - a energia nuclear. Para entender a origem desta energia, observe os dados da tabela 2. Sabemos que o átomo do deutério é igual ao átomo do hidrogênio acrescido de um nêutron. Esses dados mostram algo intrigante: a soma da massa do átomo de hidrogênio com a massa de um nêutron é maior do que a massa do deutério, como ilustra a figura 2.

Figura 2 - O átomo do deutério é igual ao átomo do hidrogênio acrescido de um nêutron.
A massa dos componentes em separado - um átomo de hidrogênio mais um nêutron - é maior do que a massa do deutério, que tem esses mesmos componentes.
Fonte: http://holbert.faculty.asu.edu/eee460/massdefect.html

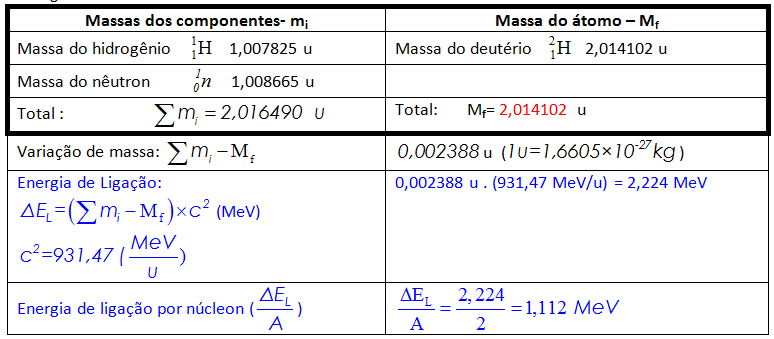
Os cálculos estão resumidos na tabela 2. Na teoria da relatividade restrita de Einstein, massa e energia são equivalentes. Uma variação da massa de um sistema (

) equivale a uma variação da energia (

) de repouso do sistema, de acordo com a relação

, em que c é a velocidade da luz no vácuo. Essa variação de massa (que, neste exemplo, vale

u) ocorre com o núcleo de todos os átomos, e equivale à energia que mantém os prótons e nêutrons unidos no interior do núcleo, ou seja, é a energia de ligação (

E_L) desse núcleo. Assim, para separar as partículas que compõem o núcleo, teríamos que fornecer ao núcleo uma energia

E_Ldurante o processo de separação. Mas o que realmente importa é a energia de ligação por núcleon (

E_L/A), ou seja, a energia média necessária para arrancar um nucleon do núcleo.

Tabela 2 - Variação de massa (energia) para a formação de um átomo de deutério.

Para compensar as massas dos elétrons, os cálculos são realizados utilizando-se a massa atômica dos átomos neutros de hidrogênio e deutério.

Para o caso do átomo de deutério, temos que a variação de massa do deutério é

u, correspondente a uma energia de ligação

E_L=2,224 MeV. Como o deutério tem dois nucleons (A=2), sua energia de ligação por núcleon é:

É muito menor, por exemplo, que a energia de ligação por nucleon do Urânio-238 (²³⁸U), como mostra a figura 2 em um gráfico bastante significativo para a física moderna. Nesta figura, o pico acentuado para A=4 mostra a estabilidade excepcional da estrutura do

(partícula alfa).

A informação mais importante da figura 3 é a consequência da transmutação de núcleos de átomos localizados nas regiões do início ou do fim da curva (núcleos menos estáveis), onde a razão () é mais baixa que a das regiões intermediárias.

Figura 3 - Energia de ligação por nucleon (

) em função do número de massa (A=Z+N). A energia de ligação por núcleon do Urânio-238 (²³⁸U) é muito maior que a energia de ligação por núcleon do deutério (²H). No processo de fissão, um núcleo pesado se divide em dois fragmentos cuja energia de ligação por nucleon é maior que a do núcleo original (em torno de 0,9 MeV).
Fonte: http://holbert.faculty.asu.edu/eee460/massdefect.html

Os núcleos que aparecem na parte superior da curva são os mais estáveis, já que é necessária uma energia maior por nucleon para desintegrá-lo. Assim, a liberação de energia na transmutação nuclear (transformar um elemento em outro por fissão ou por fusão) ocorre na passagem de um estado de menor para outro de maior energia de ligação. Os núcleos situados na extremidade direita da curva perdem massa ao se transformarem em dois núcleos com um número de massa intermediário. Este processo é conhecido como fissão. Os nucleons situados na extremidade esquerda da curva, isto é, com um número de massa pequeno, perdem massa ao se combinarem para forma um único núcleo com um número de massa intermediário. Este processo conhecido como fusão, ocorre naturalmente no interior das estrelas.

A energia Q de uma reação envolvendo produtos nucleares iniciais com massa de repouso total m_i (massa total do sistema antes da reação) e finais com massa de repouso total m_f (massa total depois da reação) é dada por:

(energia da reação)

Para levar em conta a contribuição dos elétrons, devemos usar as massas dos átomos neutros nestas equações. Ou seja, aplicamos a massa do hidrogênio

para um próton, a massa do deutério

para um dêuteron, a massa do

para uma partícula alfa (núcleo de hélio-4), e assim por diante.

A reação pode ser endotérmica (Q< 0) ou exotérmica (Q > O). Quando Q é positivo, a massa total diminui e a energia cinética aumenta. Quando Q é negativo, a massa total aumenta e a energia cinética diminui, neste caso, a reação só pode ocorrer quando a energia cinética inicial no sistema de referência do centro de massa é maior do que

. Ou seja, nesse caso existe uma energia limite - uma energia cinética mínima para que uma reação endotérmica se desencadeie.

2.1 O Ciclo próton-próton (núcleos de hidrogênio)

O exemplo mais importante de reações de fusão nuclear é a fusão de núcleos de átomos de hidrogênio em núcleos de hélio, num ciclo chamado próton-próton, que é a origem da energia do sol e, portanto, da vida no nosso planeta (veja figura 4).

Figura 4 - Esquema do ciclo próton-próton responsável pela produção de energia no Sol.
Fonte: http://pt.wikipedia.org/wiki/Cadeia_pr%C3%B3ton-pr%C3%B3ton

Na transmutação (I), o pósitron (e+) aniquila-se ao combinar com o elétron (e^-) do hidrogênio, dando origem a dois fótons de raios gama. Nessa transmutação, é liberada uma energia de 1,02 MeV; na transmutação (II), ocorre uma liberação de 5,49 MeV de energia, e na transmutação (III) liberam-se aproximadamente 12,86 MeV de energia. Como ocorrem duas reações do tipo (I) e (II), a energia total liberada no ciclo fica em torno de 26,7 MeV (energia líquida liberada por evento).
Refazendo os cálculos utilizando a equação para a energia de reação, temos:

Onde 4,002603 u é a massa de um átomo de hélio, e 1,007825 u é a massa de um átomo de hidrogênio. Os neutrinos têm massa de repouso insignificante, e a massa de repouso dos raios gama é zero: assim, estas partículas não entram no cálculo da energia de reação.

Este mesmo valor é obtido somando-se os valores de Q para os diferentes estágios do ciclo próton-próton na figura 3. Desse modo,

Q=(2)(0,42 MeV) + (2)(1,02 MeV) + (2)(5,49 MeV) + 12,86 MeV
Q=26,7 MeV

Cerca de 0,5 MeV desta energia é removida do Sol pelos dois neutrinos; o resto (26,2 MeV) é incorporado ao centro do Sol na forma de energia térmica. Esta energia térmica é gradualmente transportada para a superfície solar, de onde é irradiada para o espaço na forma de ondas eletromagnéticas, entre elas, a luz visível.

Mas como produzir uma quantidade considerável de energia nuclear na Terra?

3. A FUSÃO NUCLEAR "CONTROLADA"

A primeira reação termonuclear terrestre aconteceu no atol de Eniwetok em 1º de novembro de 1952, quando os Estados Unidos detonaram uma bomba hidrogênio (veja figura 5), liberando uma energia equivalente a 10 milhões de toneladas de TNT (1.000 vezes superior à bomba de fissão de Hiroshima).

Figura 5 - Bomba de fusão(hidrogênio) detonada no atol de Eniwetok em 1º de novembro de 1952.
O atol de Eniwweetok no Pacífico, sobre o qual foi detonada, desapareceu completamente numa cratera de mais de 500 m de profundidade e mais de 2 km de extensão. As altas temperaturas e densidades necessárias pra iniciar a reação foram conseguidas usando uma bomba de fissão como espoleta.
Fonte: Imagens Google.

Uma fonte constante e controlada de energia de fusão é considerada por muitos a fonte de energia do futuro, pelo menos para a produção de eletricidade, mas ainda é um objetivo difícil de ser atingido. O ciclo p-p ilustrado na figura 3 funciona bem, mas apenas no Sol, por causa da enorme concentração de prótons (núcleos de hidrogênio) (prótons) que existe no seu núcleo. Assim, intensos esforços vêm se desenvolvendo em muitos laboratórios para se obterem reações de fusão controladas, principalmente entre núcleos de isótopos do hidrogênio, como o deutério e trítio. Nestes reatores, já se consegue obter temperaturas da ordem de 100 milhões de kelvin (seis a sete vezes a temperatura do núcleo do Sol). Nestas temperaturas, os átomos leves ficam completamente ionizados (perdem todos seus elétrons), formando um plasma composto de núcleos e elétrons livres. Os núcleos dos átomos de deutério e trítio são chamados de dêuteron e Tríton, respectivamente.

O fato de o plasma ser constituído por partículas carregadas(dêuterons, trítons, prótons, elétrons) faz com que ele possa ser confinado por campos magnéticos em reatores chamados tokamak. Em outro tipo de experiência que usa confinamento inercial, pequenas esferas do material que deve sofrer fusão são aquecidas por feixes de laser com intensidade extremamente elevada. A ideia do confinamento é manter o plasma distante das paredes do reator que confina o plasma, pois nenhum material conhecido da parede do reator suportaria as temperaturas necessárias para que ocorra uma reação de fusão.

Algumas das reações que estão sendo experimentadas são mostradas na tabela 3:

Tabela 3 - Reações de fusão mais promissoras para uso terrestre.

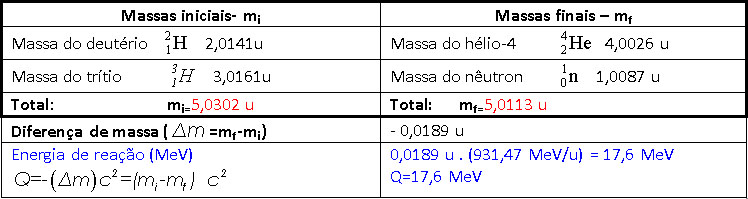
3.1 A Reação de fusão entre os núcleos de deutério e tríto (dêuteron - triton)

Nesta reação, os núcleos do deutério e do trítio,

(dêuteron) e

(tríton) se fundem para formar um núcleo de hélio

e um nêutron, de acordo com a seguinte equação:

Vamos, então, determinar a energia liberada (Q) nesta reação de fusão, ilustrada na figura 6.

Figura 6 - Em altas temperaturas, os núcleos de deutério e trítio se fundem para formar um núcleo de hélio, com a emissão de um nêutron. O resultado é a liberação de uma enorme quantidade de energia, que se manifesta principalmente na energia cinética do nêutron.

Fonte: http://pt.wikipedia.org/wiki/Fus%C3%A3o_nuclear.

Como é liberada energia, a massa total das partículas finais deve ser menor que a massa das partículas iniciais, como mostra a figura 6 e a tabela 4.

Tabela 4 - Energia de reação da fusão entre o deutério e o trítio.

O núcleo de deutério contém 2 nucleons, e o núcleo de trítio contém 3 nucleons. Assim, 5 nucleons participam da reação de fusão, e a energia liberada por núcleo é aproximadamente 3,5 MeV (veja figura 6). Essa energia por nucleon é maior que a energia liberada no processo de fissão (aproximadamente 0,9 MeV). Como mostra a figura 3, os núcleos pesados na extremidade direita da curva têm energia de ligação da ordem de 7,6 MeV por nucleon, enquanto os fragmentos mais leves na região central da curva têm uma energia de ligação da ordem de 8,5 MeV por nucleon. A energia liberada por nucleon na fissão de um núcleo pesado é igual à diferença entre estes dois valores, ou seja, cerca de 0,9 MeV por nucleon. Assim, para uma dada massa de combustível, uma reação de fusão produz mais energia que uma reação de fissão.

2.3 Sequências de reações de fusão

a) Na reação de fusão entre dois dêuterons, pode-se formar um tríton e um próton, liberando uma energia em torno de 4,0 MeV, com mostra a figura 7. Na sequência, a reação ilustrada na figura 7 pode se repetir se o tríton gerado encontrar um dêuteron em uma reação de fusão.

Figura 7 - Na reação de fusão entre dois dêuterons, formam-se um tríton e um próton. Na sequência, o tríton se combina com um dêuteron para formar uma partícula alfa (núcleo de hélio 4) e um nêutron. O resultado destas duas reações combinadas é a conversão de dois dêuterons em uma partícula alfa, um próton e um nêutron, liberando 21,6 MeV de energia.

b) Na reação de fusão entre dois dêuterons também se pode formar um núcleo de hélio-3 e um nêutron, liberando uma energia em torno de 3,3 MeV, com mostra a figura 8. Na sequência, se o núcleo de hélio-3 gerado encontrar um dêuteron em uma reação de fusão, formam-se novamente um núcleo de hélio-4 e um próton liberando uma energia de 18,3 MeV.

Figura 8 - Na reação de fusão entre dois dêuterons, formam-se um núcleo de hélio-3 e um nêutron, liberando 3,3 MeV de energia. Na sequência, o hélio 3 se combina com um dêuteron para formar uma partícula alfa (núcleo de hélio-4) e um próton (núcleo do hidrogênio). O resultado destas duas reações combinadas é a conversão de dois dêuterons em uma partícula alfa, um próton e um nêutron, novamente liberando 21,6 MeV de energia.

O resultado destas duas reações combinadas produz novamente uma energia de 21,6 MeV. Assim, em um plasma que contém dêuterons, os dois pares de reações ocorrem com a mesma probabilidade. Mas até a presente data, ninguém conseguiu produzir essas reações de modo controlado para obter um excesso de energia para ser usado. Ou seja, por enquanto, os reatores a fusão ainda consomem mais energia do que geram. O ITER (International Thermonuclear Experimental Reactor) consiste numa central de fusão nuclear planejada para gerar mais energia do que consome por confinamento magnético do plasma (tokamak). O campo magnético de 5,3 T será produzido por bobinas supercondutoras e a corrente nominal de plasma é de 15 MA, gerando em torno de 500 MW de potência de fusão. Localizado em Cadarache, na França, o ITER deverá entrar em operação no ano de 2016.