|
1. UM MUNDO DE INCERTEZAS Em 1913, ao elaborar um modelo de átomo para o Hidrogênio que permitisse justificar os resultados experimentais obtidos para os espectros de emissão desse elemento, Neils Bohr sugeriu que o elétron só pode ocupar órbitas quantizadas, isto é, órbitas cujo raio r respeitem o postulado
onde o produto m.v.r corresponde
ao momento angular do elétron e h é
a constante de Planck.
onde
Veja também a animação:
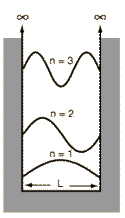
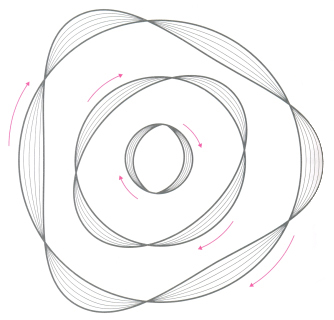
Figura 2: Ondas estacionárias dos elétrons
nas três primeiras órbitas de um átomo de hidrogênio.
Para que a onda associada ao movimento do elétron
possa caber na circunferência correspondente à órbita
quantizada, o perímetro da órbita de raio r deve conter
um número inteiro de comprimentos de onda de De Broglie,
ou ou
Mas p.r =m.v.r é o momento
angular do elétron considerado como partícula, ou
seja,
e a interpretação ondulatória conduz naturalmente ao postulado de Bohr, pois a equação 5 é idêntica à equação 1. Veja a animação:
As posições ocupadas pelo elétron
continuam quantizadas pelo número inteiro n,
como no modelo de Bohr, porém agora com uma justificativa
física associada ao comportamento ondulatório do elétron.
Dessa forma, é possível justificar os fenômenos
discretos que caracterizavam o modelo de Bohr, tal como as transições
do elétron entre duas órbitas quantizadas.
1.1 A descrição matemática das ondas de matéria: Schrödinger e a função de onda do elétron A natureza dual da matéria pode ser expressa
matematicamente por meio de uma equação de onda. Erwin
Schröedinger, em 1926, desenvolveu a Mecânica Quântica,
cujo resultado principal é a equação que descreve
o elétron por uma função de onda
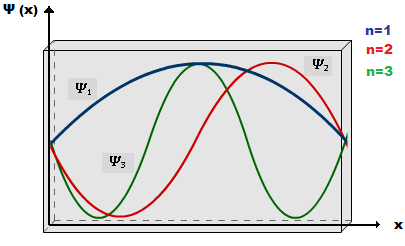
Figura 3: Ondas estacionárias associadas
a uma partícula presa dentro de uma caixa de largura L.
Para localizar a partícula numa dada posição x dentro da caixa, precisamos encontrar as funções de ondas estacionárias que descrevem o movimento da partícula. Obviamente, a partícula não pode estar localizada no exterior da caixa, o que significa que a função de onda toma o valor zero nessa região, isto é,
Para que uma mesma partícula tenha comprimentos de onda diferentes, associados ao seu movimento, deve ter energias diferentes. O menor valor de energia é obtido substituindo n por 1 e o estado da partícula correspondente a este valor de n é conhecido como estado fundamental. O primeiro estado excitado está associado com n = 2 e, assim, sucessivamente. Ou seja, os comprimentos de onda e as energias permissíveis são discretos e esta é a razão pela qual, na mecânica quântica, uma partícula confinada, assim como o elétron em órbitas atômicas, só pode ter certas energias!
A figura 4 mostra as três primeiras funções
de onda
Figura 4: Representação das três primeiras funções de onda para uma partícula numa caixa unidimensional.
Max
Born (1928) propôs uma interpretação
estatística das funções de onda associadas
ao movimento de partículas. Born supôs que as ondas
não têm existência real e, assim, as define como
ondas de probabilidade. Assim, o módulo da função
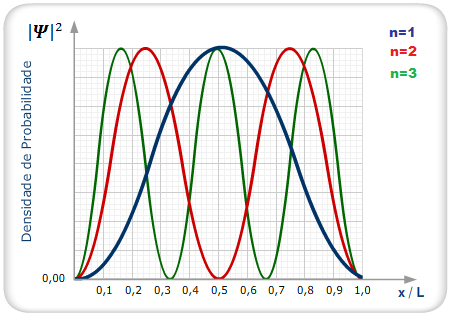
A figura 5 mostra a representação
do resultado de
Figura 5: Representação da densidade
de probabilidade
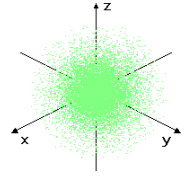
A visualização tridimensional da
função densidade de probabilidade
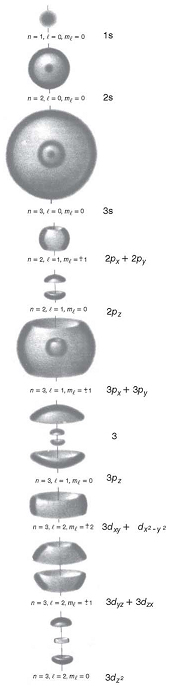
Mas a representação mais utilizada
de
Figura 7: Representação visual dos
estados estacionários do elétron em um átomo
de hidrogênio. Vale ressaltar que essa é uma representação
pictórica dos orbitais, decorrente de nossa necessidade de
visualização do interior do átomo. O grande
mérito da Mecânica Quântica consiste em descrever
o comportamento dos componentes do átomo através de
equações que não só nos permitem explicar
os resultados experimentais, mas também prever o comportamento
de um conjunto de átomos, seja em estruturas cristalinas,
seja em moléculas complexas, possibilitando também
a compreensão de fenômenos químicos e biológicos.
Dessa maneira, podemos dizer que a Mecânica Quântica
é a teoria que mais obteve sucesso na física, proporcionando
uma melhor compreensão da natureza e descobertas tecnológicas
que estão na base de muitos equipamentos que não dispensamos
no nosso cotidiano. REFERÊNCIAS
|

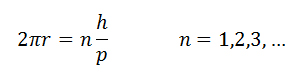 (3)
(3)