A descoberta dos números irracionais

Foi por meio do Teorema de Pitágoras que os números irracionais começaram a ser introduzidos na Matemática. O primeiro irracional a surgir foi √2, que apareceu no cálculo da hipotenusa de um triânguloângulo com catetos medindo 1.

Veja o exemplo abaixo:

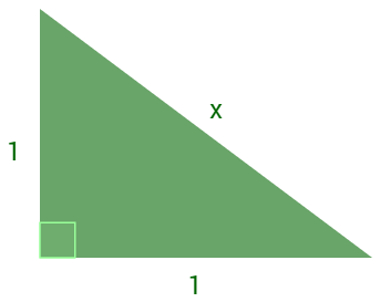
x² = 1² + 1²

x² = 1 + 1

x² = 2

√x² = √2

x = √2

x = = 1,414213562373.

1º) Calcule o valor do cateto no triângulo retângulo abaixo:

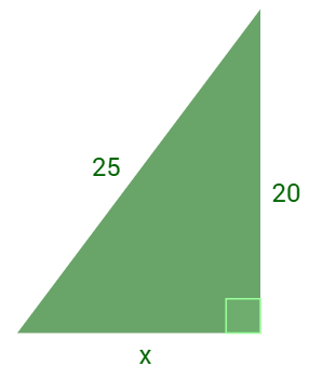
2º) Calcule o valor do segmento desconhecido no triângulo retângulo a seguir.

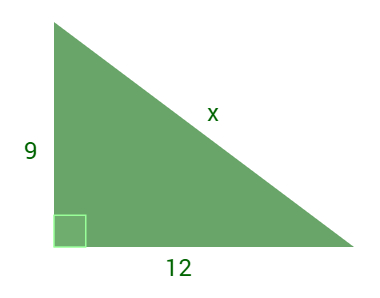
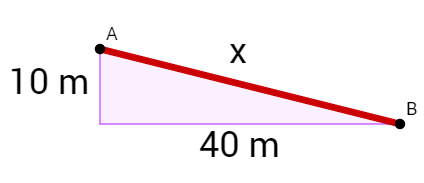
3º) Um ciclista acrobático passará de um prédio a outro com uma bicicleta especial e sobre um cabo de aço, como demonstra o esquema a seguir:

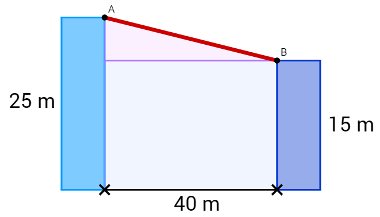
Qual é a medida mínima do comprimento do cabo de aço?

Teorema de Tales

Tales de Mileto foi um importante filósofo, astrônomo e matemático grego que viveu antes de Cristo. Ele usou seus conhecimentos sobre Geometria e proporcionalidade para determinar a altura de uma pirâmide. Em seus estudos, Tales observou que os raios solares que chegavam à Terra estavam na posição inclinada e eram paralelos, dessa forma, ele concluiu que havia uma proporcionalidade entre as medidas da sombra e da altura dos objetos, observe a ilustração:

Com base nesse esquema, Tales conseguiu medir a altura de uma pirâmide com base no tamanho da sua sombra. Para tal situação ele procedeu da seguinte forma: fincou uma estaca na areia, mediu as sombras respectivas da pirâmide e da estaca em uma determinada hora do dia e estabeleceu a proporção:

O Teorema de Tales pode ser determinado pela seguinte lei de correspondência:

“Feixes de retas paralelas cortadas ou intersectadas por segmentos transversais formam segmentos de retas proporcionalmente correspondentes”.

Para compreender melhor o teorema observe o esquema representativo a seguir:

Pela proporcionalidade existente no Teorema, temos a seguinte situação:

Exemplo 1
Aplicando a proporcionalidade existente no Teorema de Tales, determine o valor dos segmentos AB e BC na ilustração a seguir:

AB = 2x - 3
BC = x + 2
A’B’ = 5
B’C’ = 6

Determinando o valor de x:


AB = 2x - 3 → 2*4 - 3 = 5
BC = x + 2 → 4 + 2 = 6