UNIJUÍ : UNIVERSIDADE REGIONAL DO
NOROESTE DO ESTADO DO RIO GRANDE DO SUL
DeFEM : DEPARTAMENTO DE FÍSICA, ESTATÍSTICA
E MATEMÁTICA
CONSTRUÇÃO CIVIL
ANA MARIA SCARTON
ALISSON RENZ
SERLI B. CASSEL
MODELAGEM MATEMÁTICA I
PROFESSOR: PEDRO A. P. BORGES
IJUÍ (RS), DEZEMBRO DE 2001
INTRODUÇÃO
O
tema Construção Civil que nos propomos pesquisar envolve vários conteúdos de
matemática. Por isso, é uma ferramenta que pode ser usada pelo professor para
tornar sua aula mais interessante e proporcionar aos alunos uma relação entre
a matemática estudada em sala de aula com a matemática real utilizada na resolução
de problemas do cotidiano.
Essa pesquisa também nos possibilitará
conhecer uma nova tendência dentro do ensino da Matemática, que pode ser útil
no exercício de nossa profissão, além de proporcionar ao aluno a criatividade
e pesquisa e a busca de resolução de problemas.
Para realizarmos esta pesquisa,
primeiramente elaboramos a planta baixa da casa, definimos suas medidas e a
partir disso elaboramos as questões/situações problemas para modelarmos. Dentre
os tópicos de matemática que utilizamos para o modelo estão: Geometria e Números
Racionais.O tema nos possibilita criar modelos matemáticos genéricos para serem
utilizados em qualquer construção civil.
Salientamos que nossa investigação
ficou restrita a algumas partes da Construção Civil, tendo em vista a complexidade
e extensão de sua abordagem, ficando então aberto a possibilidade de novas/futuras
pesquisas. Acreditamos que esta investigação é importante pois nos dá condições
de determinar a quantidade de material necessário para uma construção, evitando
assim, o desperdício de material, bem como termos condições de comparar diferentes
modelos de construção como por exemplo: a comparação entre o custo de uma parede
feita com tijolos a vista e uma parede feita com reboco.
Elaboração da Planta
Para elaborarmos a planta baixa,
definimos primeiramente os cômodos e suas medidas reais.
Utilizamos a escala
de 1:50, isto é: cada 1m no papel corresponde a 0,50m na medida real.
Os modelos matemáticos abaixo
nos auxiliam na transformação das medidas reais da planta em medidas no desenho,
ou vice versa.
MR=(MDx100)/2
MD=(2xMR)/100
MD = Medida no Desenho
MR
= Medida Real da planta
Por Exemplo:Se tomarmos as medidas
da sala , utilizando o modelo temos:
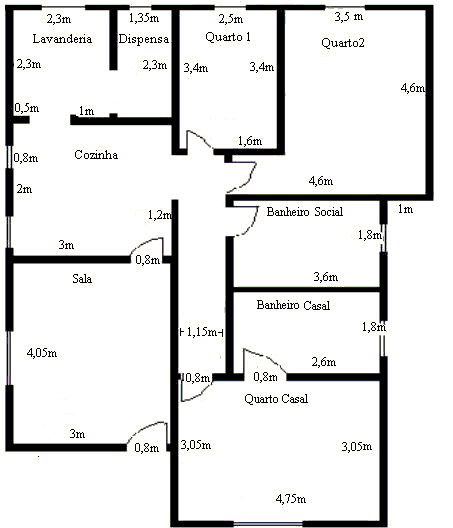
DESENHO DA PLANTA BAIXA

A1
= Área 1
A2
= Área 2
AT
= Área Total
1.1 Qual a área total da casa
O modelo abaixo nos possibilita calcular a área de qualquer superfície
em forma retangular:
A=CxL onde
C= Comprimento
L= Largura
Como
o desenho da casa é uma figura irregular, precisamos calcular a área da figura
A1 e da figura A2 para depois somá-las, obtendo-se a área
total (AT) da casa.
A1
= C x L
A2 = C x L
AT = A1 + A2
A1
= 12m x 8 m A2
= 4,6 m x 1 m
AT = 96m2 + 4,6 m2
A1 = 96 m2
A2 = 4,6m2
AT = 100,6 m2
1.2 Qual a área
total da lavanderia?
Pelo
desenho podemos verificar que a lavanderia possui a medida de seus lados iguais.
Para sabermos a área total da lavanderia podemos utilizar os seguintes modelos
matemáticos:
AT
= LxL ou
AT=L2
,
onde L = Lado e AT
= Área Total
AT
= 2,3 m x 2,3 m
AT =( 2,3 m)2
AT
= 5,29 m2
AT = 5,29m2
1.3 Qual o perímetro da casa?

Sendo
o perímetro a soma de todos os segmentos, seu cálculo poderá ser feito assim:
P = 9m + 4,6m
+ 1m + 7,4m + 8m + 12m
P =42
m
1.4 Qual o perímetro da lavanderia?
Modelo
matemático:
P
= L + L + L + L =>
P=2,3m
+ 2,3m + 2,3m + 2,3m = 9,2 m
ou
P= 2(L1+L2)
=> P = 2 (2,3m + 2,3m) = 9,2m
3- AZULEJOS
Com base nos modelos de área
já construídos, calcularemos os seguintes problemas em relação aos azulejos:
3.1. Qual a quantidade de azulejos por m2?
Largura
de um azulejo de forma quadrada: 30cm + 0,25cm = 30,25cm
A= L2
= (30,25cm)2
= 916,0625cm2
Metro quadrado: 100cm
x100cm
Área= L2
A= (100cm)2
= 10.000cm2
Calculando a quantidade de azulejo
por metro quadrado:
Qt= AM/Am onde
AM= área maior
QT= 10.000cm2 / 916,0625cm2
3.2 Para calcular a área total
de um cômodo cujas paredes serão revestido por azulejos
At= Pc x hc - Aab, onde
At= Área total a ser revestida;
Pc é o perímetro do cômodo;
hc é a altura das paredes do cômodo e
Aab é a área ocupada pelas aberturas.
Como
calcular o número de azulejos necessários?
Qt=
At /Az, onde At=área total
Exemplo
3.3 Calculando o número
de azulejos para revestir as paredes da lavanderia
Azulejo
= 30cm x 30cm
reboco = 0,25cm (distância entre os azulejos)/2
Az=(30,25)2
= 915,0625cm2
Aberturas:
Área das duas portas = 2x(210cm
x 80cm)
Área da Janela = 80cm x
70cm
Aab = 2xAp + Aj, onde Ap = Área da Porta e Aj = Área da Janela
Aab = 39200cm2
At=
Pc x hc
- Aab, onde
At
= 209200cm2 =
20,92m2
Quantidade de Azulejos
Qt=At/Az=209200cm2/(915,0625cm2/azulejo) = 228 azulejos.
Obs. Nestes cálculos considera-se que todos os azulejos teriam aproveitamento de 100%. Isto significa que partes da parede ficariam com azulejos não inteiros. Esteticamente, isto não fica bem.
O problema que se poderia fazer em seguida, poderia o uso das medidas do azulejo, como unidade de medida da parede.
