ANÁLISE DAS CONDIÇÕES DE PAGAMENTO DO FINANCIAMENTO DO PLANTIO DA SOJA CONSIDERANDO AS MUDANÇAS CLIMÁTICAS NA SAFRA 2004.
Erivelto Quadros 1
Vera Regina Danette 2
Este artigo desenvolve uma pesquisa a respeito do plantio da cultura da soja safra 2004 feito através de um programa de financiamento em que é utilizado a modelagem matemática para analisar as condições de pagamento do mesmo.
Diante dos desafios que a educação matemática nos apresenta hoje é imprescindível que se busque meios/alternativas as quais possam nos auxiliar para que consigamos chegar a um ensino matemático, que além de satisfazer as necessidades do aluno, venha em primeiro posto despertar o interesse e o reconhecimento que se faz necessário ao desenvolvimento do ensino em matemática pelos alunos.
Uma dessas alternativas é a modelagem matemática que é a arte de usar a matemática para expressar um problema real. A utilização da modelagem matemática no ensino tem como principal objetivo despertar o interesse e a criatividade dos alunos pois ela propicia ao aluno a oportunidade de estudar situações- problemas por meio de pesquisa, desenvolvendo seu interesse e aguçando seu senso crítico.
Nesse sentido, escolhemos uma situação- problema que envolve a cultura da soja, feita através de um programa de financiamento, levando em consideração as mudanças climáticas que ocorreram na safra 2004 para aplicarmos a modelagem. Para isso vamos introduzir o conteúdo explicitando em primeiro lugar o programa de financiamento utilizado, o projeto apresentado pelo agricultor por meio de um agrônomo e os produtos necessários para a cultura da soja.
O programa de financiamento utilizado pelo agricultor foi o PROGER- custeio agrícola via banco – do governo federal. Para usufruir dessa modalidade de financiamento o agricultor tem que ter no mínimo 60 ha e no máximo 240 ha e apresentar um projeto elaborado por um agrônomo, que seja devidamente habilitado. O projeto deve conter: relação de máquinas e equipamentos agrícolas que o agricultor possui; financiamento proposto- no caso a cultura da soja; discriminação dos itens a serem financiados e análise da situação financeira do cliente (receita).
No PROGER o PRO-AGRO- que é o seguro agrícola- é opcional 2,9 % sobre o valor total do empréstimo, isto é, essa porcentagem é descontada do financiamento quando houver uma grande perda na produção ocasionada por fatores climáticos; a taxa de juro é de 8,417532% ao ano e o prazo para quitação do mesmo é em torno de 9 meses, isto é, vai do plantio até a colheita.
O crédito concedido é o valor do projeto apresentado não podendo ultrapassar o valor de R$ 612,00 por ha.
A seguir demonstraremos um exemplo de um projeto de empréstimo com objetivos e prazos determinados:
Hectares Financiados: 78ha.
Valor do Empréstimo: R$ 47.736,00
Liberado em duas parcelas: 1ª R$ 42.962,40 (90% do valor total) em 15/10/2004 e 2ª R$ 4.773,60 ( 10% restantes) em 06/03/2005.
Tabela 01: Orçamento do Projeto para 78 ha
| DESCRIÇÃO |
QUANT. |
UNID. |
V. UN. |
V. TOT |
| Sementes |
78 |
scs |
50,00 |
3.900,00 |
| Fert. de Base |
19.500 |
kg |
0,89 |
17.355,00 |
| Inseticida |
15,60 |
lt |
76,00 |
1.185,60 |
| Dessecante |
117 |
lt |
14,00 |
1.638,00 |
| Pré- Emergentes |
78 |
lt |
66,91 |
5.218,98 |
| Pós- Emergentes |
31,2 |
lt |
110,00 |
3.432,00 |
| Fung. Trat. Sem. |
19,5 |
lt |
50,00 |
975,00 |
| Fung. Parte Área |
58,5 |
lt |
105,00 |
6.142,50 |
| Dessecação |
78 |
ha |
6,34 |
494,52 |
| Semead/Adubação |
78 |
ha |
30,00 |
2.340,00 |
| Aplic. Herbicida |
78 |
ha |
6,40 |
499,20 |
| Aplic. Inset/Fung. |
78 |
ha |
6,40 |
499,20 |
| Colheita |
78 |
ha |
40,00 |
3.120.00 |
| Assist. Técnica(1) |
78 |
ha |
12,00 |
936,00 |
| TOTAL DESPESAS |
|
|
|
R$ 47.736,00 |
DESCRIÇÃO DO PROBLEMA:
Qual é a estimativa de lucro do produtor em um ano com clima favorável? E qual o seu prejuízo em caso de clima desfavorável como 2004?
Qual o valor que ele terá que pagar ao banco sabendo que o empréstimo vence em 15/06/2005 e que a taxa de juro é de 8,417532 % ao ano?
Qual o desconto que esse produtor teria se ele resolvesse quitar o empréstimo na metade do mês?
Qual a produtividade mínima por ha para que o produtor possa pagar o financiamento?
RESOLUÇÃO DO PROBLEMA
Tabela 02: Custo de Produção da soja por 1 ha
| DESCRIÇÃO |
QUANT. |
UNID |
V. UN. |
V. TOT. |
| Sementes |
1 |
scs |
50,00 |
50,00 |
| Fert. de Base |
250 |
kg |
0,89 |
222,50 |
| Inseticida |
0,2 |
lt |
76,00 |
15,20 |
| Dessecante |
1,5 |
lt |
14,00 |
21,00 |
| Pré- Emergentes |
1 |
lt |
66,91 |
66,91 |
| Pós- Emergentes |
0,4 |
lt |
110,00 |
44,00 |
| Fung. Trat. Sem |
0,25 |
lt |
50,00 |
12,50 |
| Fung. Parte Área |
0,75 |
lt |
105,00 |
78,75 |
| Dessecação |
1 |
ha |
6,34 |
6,34 |
| Semead/Adubação |
1 |
ha |
30,00 |
30,00 |
| Aplic. Herbicida |
1 |
ha |
6,40 |
6,40 |
| Aplic. Inset/Fung |
1 |
ha |
6,40 |
6,40 |
| Colheita |
1 |
ha |
40,00 |
40,00 |
| Assist. Técnica (1) |
1 |
ha |
12,00 |
12,00 |
| TOTAL DESPESAS |
|
|
|
R$ 612,00 |
Qual é a estimativa de lucro do produtor em um ano com clima favorável? E qual o seu prejuízo em caso de clima desfavorável?
A média de produção da soja na nossa região é de 40 scs/ha (a produção gira em torno de 35 a 45 scs/ha).
O lucro desse produtor em um ano de clima favorável é de 3120 scs. O preço da saca de soja (60kg) hoje é de R$ 31,00. O produtor teria um lucro de R$ 96.720,00, ou seja, um lucro de R$ 1.240,00 por ha.
Em um ano de clima desfavorável, como é caso desse ano, a colheita da soja foi muito prejudicada. A média de produção caiu de 40 scs por ha para 10scs ( a produção está girando em torno de 8 a 12 scs/ha). Sua produção seria de 780 scs. Em R$ 24.180,00. Esse produtor teria um prejuízo de 2340 scs, ou seja, seu prejuízo seria de R$ 72.540,00.
Gráfico 01: Comparação da produção da soja levando em consideração os fatores climáticos

Qual o valor que ele terá que pagar ao banco sabendo que o empréstimo vence em 14/06/2005 e que a taxa de juro é de 8,417532 % ao ano?
O produtor retirou o empréstimo em 15/10/04 e 06/03/05 totalizando R$ 47.736,00. O prazo para quitação do mesmo é de 9 meses.
Sabemos que:



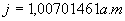
mês 1=

mês 2=

mês 3=

.
mês n=


Onde:
Cn = Capital Final
C0= Capital inicial
j= taxa de juro aplicada
n= nº de meses
Logo substituindo os termos e calculando temos:


O valor total que o produtor terá que pagar ao banco em junho de 2005 é de R$ 50.481,49.
Observe na tabela 03 o crescimento mensal da dívida.
Tabela 03: Evolução da Dívida mês a mês
| DATA |
CAPITAL FINAL |
| 15/10/04 |
R$ 47.736,00 |
| 15/11/04 |
R$ 48.070,85 |
| 15/12/04 |
R$ 48.408,05 |
| 15/01/05 |
R$ 48.747,61 |
| 15/02/05 |
R$ 49.089,56 |
| 15/03/05 |
R$ 49.433,90 |
| 15/04/05 |
R$ 49.780,66 |
| 15/05/05 |
R$ 50.129,85 |
| 15/06/05 |
R$ 50.481,49 |
Observe o gráfico 02:
Gráfico 02: Evolução do Empréstimo

Aqui podemos perceber que o crescimento da dívida se dá de forma exponencial.
Com essa fórmula podemos calcular o valor a ser pago a qualquer mês.
Qual o desconto que esse produtor teria se ele resolvesse quitar o empréstimo na metade do mês?
Sabemos que a fórmula para calcularmos o valor total da dívida é:

Vamos supor que esse produtor queira quitar o empréstimo na metade do segundo mês após a retirada do mesmo. Assim temos:
mês 3=

mês
2,5 (dois meses e 15 dias) =

Podemos ver que esta fórmula calcula o valor a ser pago durante qualquer tempo. Mas o que queremos saber é qual o valor do desconto. Logo:
Desconto:


Assim
temos:

Onde:
D= desconto
C0= capital inicial
j= taxa de juro aplicada
n+1= mês seguinte (mês cheio)
n= mês quebrado
Substituindo os termos e calculando temos:


Caso ele resolvesse pagar na metade do segundo mês ele pagaria R$ 48.577,53. Teria um desconto de R$ 170,07.
Com essa fórmula podemos calcular o desconto que o produtor terá a qualquer tempo que ele resolva quitar o empréstimo.
Qual a produtividade mínima por ha para que o produtor possa pagar o financiamento?
O total da dívida que ele terá que pagar R$ 50.481,49.
O total de ha que ele que possui é 78 ha. Dividindo o valor total da dívida por 78 ha resulta em R$ 647,198558 por ha. Como sabemos o preço da saca da soja é de R$ 31,00 logo: dividindo R$ 647,19858 por R$ 31,00 resulta em 20,8778 scs/ha.
Ele terá que produzir no mínimo 20,8778 scs/ha, ou seja, um total de 1628,4351 scs para saldar a dívida.
Nosso objetivo com a realização deste trabalho é mostrar para as pessoas, como pode ser feito o cálculo de um empréstimo, bem como de um desconto utilizando a modelagem matemática. Pois com esse modelo, pode –se calcular qualquer o valor a ser pago a qualquer tempo inclusive o desconto do mesmo caso ele queira pagar na metade de um determinado mês
dando a oportunidade das pessoas entenderem de que forma são feitos esses cálculos pelos bancos com uma maior facilidade.
Através dessa análise desse programa de financiamento podemos perceber que podem ser trabalhados diversos conteúdos matemáticos. São eles: Intervalos e suas operações – considerando as médias de produção da soja por ha levando em conta os fatores climáticos- ; funções – principalmente a função exponencial- relação de variáveis dependentes e independentes, gráficos.
Com o modelo
 que foi elaborado para calcular o valor do empréstimo a ser pago em qualquer tempo, podemos ver que essa fórmula é a fórmula de uma Função Exponencial
(
que foi elaborado para calcular o valor do empréstimo a ser pago em qualquer tempo, podemos ver que essa fórmula é a fórmula de uma Função Exponencial
(
 com
com
 e
e
 ). Aqui podemos verificar qual a diferença entre uma função exponencial e uma P.G. Como sabemos a fórmula da P.G.
é
). Aqui podemos verificar qual a diferença entre uma função exponencial e uma P.G. Como sabemos a fórmula da P.G.
é
 ( com
( com
 e
e
 ). A diferença que ocorre é o termo no expoente. Na função exponencial ele pode assumir qualquer valor, já na P.G. ele não pode ser um valor quebrado e também tem que ser diferente de zero.
). A diferença que ocorre é o termo no expoente. Na função exponencial ele pode assumir qualquer valor, já na P.G. ele não pode ser um valor quebrado e também tem que ser diferente de zero.
Podemos ver que esse método de ensino pode ser usado nas mais variadas situações do dia- a- dia para desenvolver um conteúdo matemático propiciando ao aluno desenvolver suas potencialidades e sua capacidade de pensamento crítico e independente. Nesse sentido o aluno não só aprende a fazer modelos mas também adquire conhecimentos matemáticos.
Com o uso da modelagem o papel do professor sofre uma mudança, isto é, ele deixa de ser o transmissor do conhecimento para se tornar um facilitador da aprendizagem. O aluno passa a ser visto como centro da aprendizagem – um ser ativo. Ele aprende através da experiência e manipulação, ou seja, ele aprende fazendo.
Consideramos a modelagem matemática um método muito importante para o ensino da matemática na escola pois ele propicia ao aluno aprender a interpretar a realidade através da matemática dando a ele o domínio de determinadas habilidades ,matemáticas apara que ele possa se mover melhor e mais habilmente no meio onde vive e atuar sobre ele.
BIBLIOGRAFIA
BIEMBENGUT, Maria Salete. Modelagem Matemática e implicações no ensino aprendizagem de matemática.
1 Erivelton Quadros – Aluno do Curso de Licenciatura em Matemática da UNIJUÍ
2 Vera Regina Danette – Aluna do Curso de Licenciatura em Matemática da UNIJUÍ

