
CÁLCULO MATRICIAL DAS DESPESAS
|
Pu1 |
|
Pu2 |
|
Pu3 |
|
Pu4 |
|
... |
|
|
|
|
|
|
|
|
|
Pu n |
Q1 |
|
Q2 |
|
Q3 |
|
Q4 |
|
... |
|
|
|
|
|
|
|
|
|
qn |
CP 1 |
CP 2 |
CP 3 |
CP 4 |
... |
|
|
|
|
|
|
|
|
CP n |
Com as matrizes dispostas na forma acima não podemos realizar as devidas
multiplicações, assim sendo, poderemos transformas a primeira numa matriz
diagonalizada o numa transposta.
Qd nxn PUnx1 = CP nx1
|
Q1 |
|
|
|
|
|
|
|
|
|
|
|
Q2 |
|
|
|
|
|
|
|
|
|
|
|
Q3 |
|
|
|
|
|
|
|
|
|
|
|
Q4 |
|
|
|
|
|
|
|
|
|
|
|
... |
|
|
|
|
|
|
|
|
|
|
|
... |
|
|
|
|
|
|
|
|
|
|
|
... |
|
|
|
|
|
|
|
|
|
|
|
... |
|
|
|
|
|
|
|
|
|
|
|
... |
|
|
|
|
|
|
|
|
|
|
|
qn |
.


q1 0 0 ... 0 PU 1 CP1
0 q2 0 ... 0 PU 2 CP2



0 0 q3 ... 0 PU 3 = CP3
... ... ... ... ... ... ...
0 0 0 ... qn PU n CPn
Qd. PU = CP
QT 1x n
|
Q1 |
Q2 |
Q3 |
Q4 |
... |
|
|
|
|
Qn |
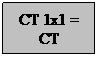
Q1 Q2 Q3 ... QN PU 1
PU 2 = CT
PU 3
...
 PU n
PU n
Ø QT:=linalg[matrix](1,4,[4,1,4,1]);
![]()
Ø PU:=linalg[matrix](4,1,[2.34,5.07,0.6,2.39]);

Ø CT:=evalm(QT&*PU);
![]()
R$ 19,22 é o custo de 10,9 kg de sabão glicerina fabricado de forma caseira
Abreviaturas usadas:
Q = quantidade
Pu = preço unitário
CP = custo parcial
Qd = quantidade (diagonalizada)
QT = quantidade (transposta)
CT = custo total
Em seguida foi realizada uma pesquisa sobre outras receitas de sabão caseiro:
