1.3.2 Racionalização de denominadores

Quando o denominador de uma fração envolve radicais, o processo pelo qual se transforma essa fração noutra cujo denominador não tem radicais chama-se racionalização de denominadores.

Exemplos:

Dicas para o uso do Geogebra

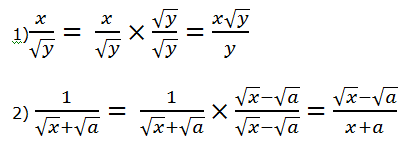
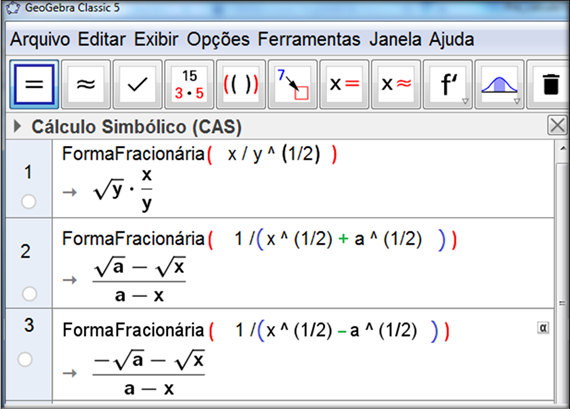
No Geogebra, para colocar expoente digita-se a base em seguida   ^ e o expoente. Para multiplicação utilize * (asterisco).  Para  divisão utilize / e para +  e  -, utilize os sinais convencionais ( + e  -)

Exemplos:

2³ digita-se 2^3 e aciona-se Enter.

2^-3 digita-se 2^(-3)e aciona-se Enter.

 Para raiz quadrada de 2 digita-se 2^(1/2) e aciona-se Enter.

Para raiz cúbica de 2 elevado ao expoente 5 digita-se 2^(5/3) e aciona-se Enter.

Em expressões com numerador (x²-9) e denominador (x-3), é preciso colocar cada termo entre parênteses caso não seja apenas um número.

   digita-se (x^2-9)/ (x+3)  e aciona-se Enter.

Exercícios envolvendo propriedades dos números reais.

Encontre o número real resultante, com o denominador racionalizado, de cada uma das expressões numéricas a seguir , caso exista.

Saiba mais sobre números reais irracionais

   
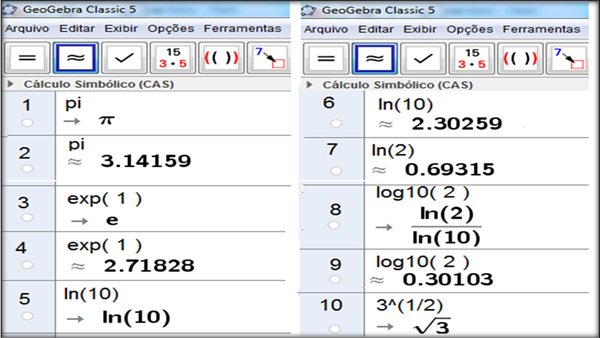
https://www.geogebra.org/classic#cas

 Para ver os valores expressos em irracionais, após a digitação, você aciona Enter ou clique no ícone    =  no Geogebra. Para obter um valor aproximado, após a digitação, você deve clicar no segundo ícone.