4. Funções Algébricas e Transcendentes
4.1 Definição e representação
Uma função matemática define uma relação de dependência duas quantidades.
Na imagem acima aparece a função um software personalizado(y) que depende do número de horas previstas para a desenvolvimento (x). Neste exemplo a variável(y) depende da variável (x). No caso, a empresa cobra R$ 100,00 por hora mais uma taxa fixa de R$ 300.00 para a definição do software desejado com o cliente.
A expressão algébrica(lei) desta função é y=100x+300 é uma das formas de representar a função.
4.2 Domínio, Imagem, análise gráfica de funções
Os valores de x que podem ser utilizados neste caso são valores a partir de 40horas e seus múltiplos. O conjunto destes valores que x pode assumir é chamado de domínio da função.
O conjunto de valores que y pode assumir é chamado de imagem da função.
Formas de representação de uma função matemática mais utilizadas são: pela lei da função ou expressão algébrica: y=100x+300, Na forma de tabelas.e Na forma de gráfico.


Como encontrar a equação/lei/expressão da função de primeiro grau se divermos dois pontos conhecidos
:http://www.projetos.unijui.edu.br/matematica/pre-calculo/Estudo_Reta_Parabola.xlsx

4.2 1 Funções Polinomiais
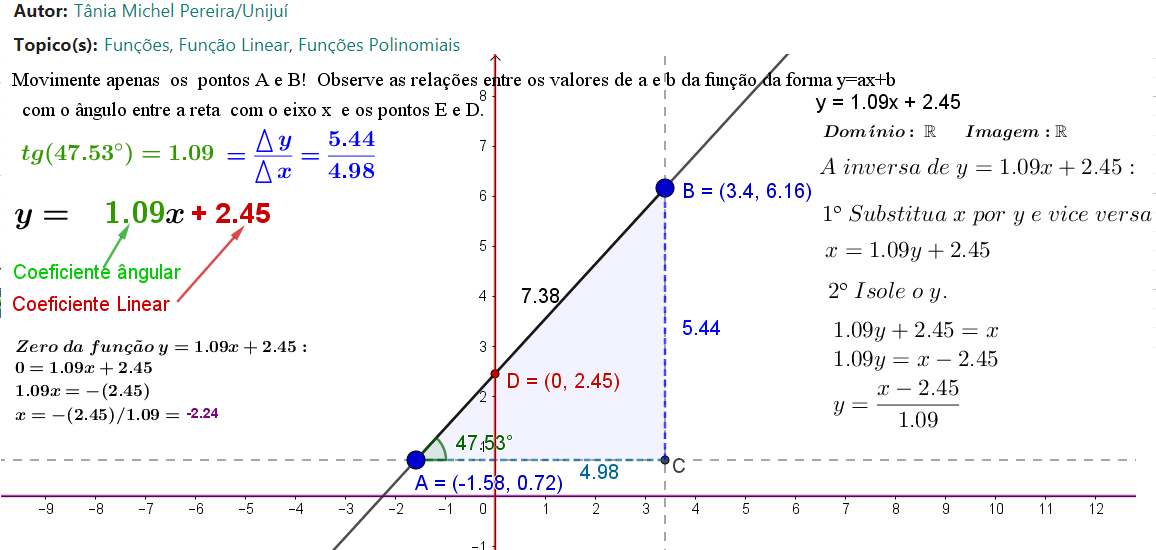
Função afim
O tipo de função que aparece na imagem inicial deste capítulo é uma função polinomial de primeiro grau ou função afim. Para ver o comportamento desta função acesse o endereço https://www.geogebra.org/m/tgemjpz6 a seguir ou na imagem e movimente o ponto Aazul. Você também pode pesquisar mais utilizando Youtube, Google acadêmico ou outro meio que você preferir.
Endereço do objeto: https://www.geogebra.org/m/yaw2m6s9
Função Quadrática: y=ax²+bx+c
A função quadrática é uma função polinomial de grau 2. O gráfico de uma função quadrática é sempre uma parábola(que pode estar voltada para cima ou para baixo) quando o domínio considerado é todo o conjunto dos reais, visto que não tem restrições para x, pois qualquer valor real pode ser multiplicado, somado e ser elevado ao quadrado. A imagem (valores que y pode assumir) e o número raízes( valores de x que anulam y) depende dos valores dos parâmetros a, b e c. Para fazer o estudo da concavidade, imagem e das raízes da função polinomial acesse o endereço a seguir ou outros que você preferir.https://www.geogebra.org/m/cmvv2et2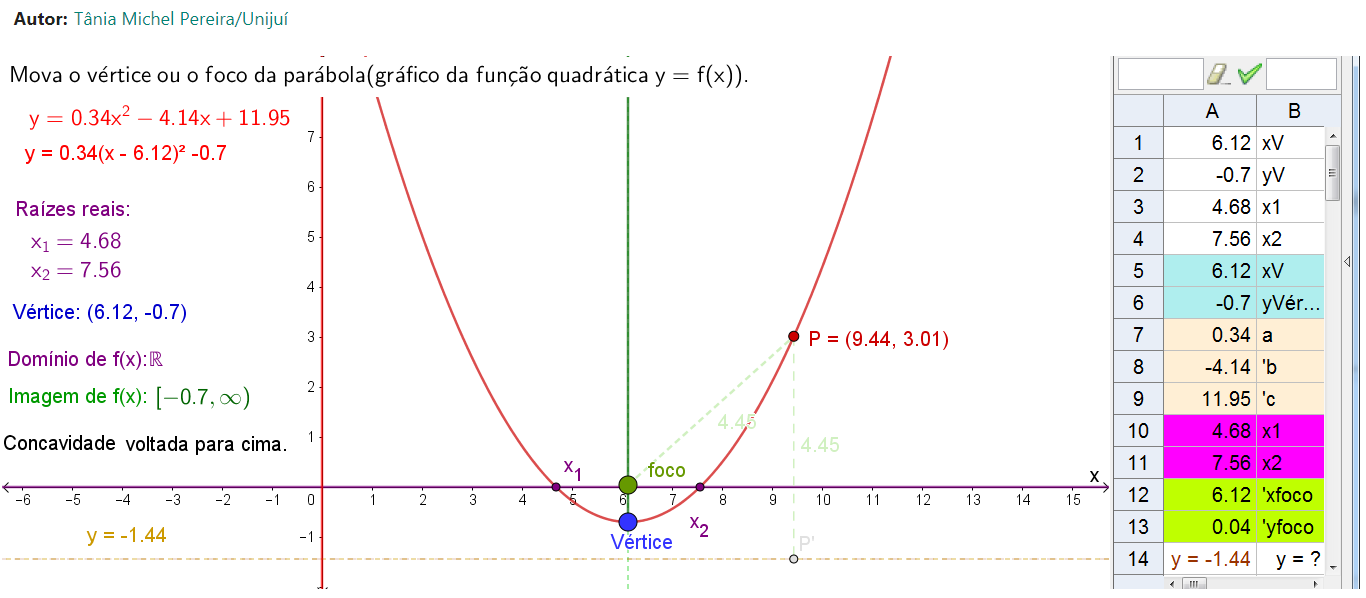
https://www.geogebra.org/m/cmvv2et2
Comparação dos gráficos de polinomiais de grau par com grau ímpar.
Acesse o endereço a seguir para ver a diferença.
 http://www.projetos.unijui.edu.br/matematica/pre-calculo/Estudo_Reta_Parabola1.xlsx
http://www.projetos.unijui.edu.br/matematica/pre-calculo/Estudo_Reta_Parabola1.xlsx
https://www.geogebra.org/m/caxvty3q
Desenvolva a atividade baixando o arquivo do Excel que se encontra no endereço a seguir para praticar exercícios envolvendo o assunto. http://www.projetos.unijui.edu.br/matematica/pre-calculo/Estudo_Reta_Parabola1.xlsx
Mais funções polinomiais Acesse o Aplicativo abaixo para ver o domínio , imagem, forma do gráfico e aogumas raíses das funções polinomiais.
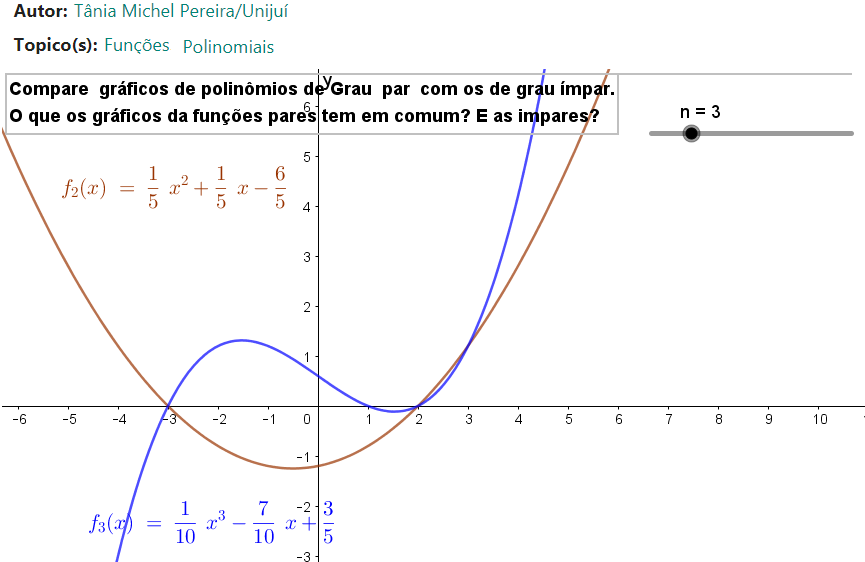
https://www.geogebra.org/m/caxvty3q
4.2.2 Racionais
Para estudar o domínio e imagem e raízes das funções racionais acesse o endereço a seguir e escolha a opção Funções Racionais.
4.2.3 Irracionais
Para estudar o domínio e imagem e raízes das funções Irracionais acesse o endereço a seguir e escolha a opção Funções Irracionais.
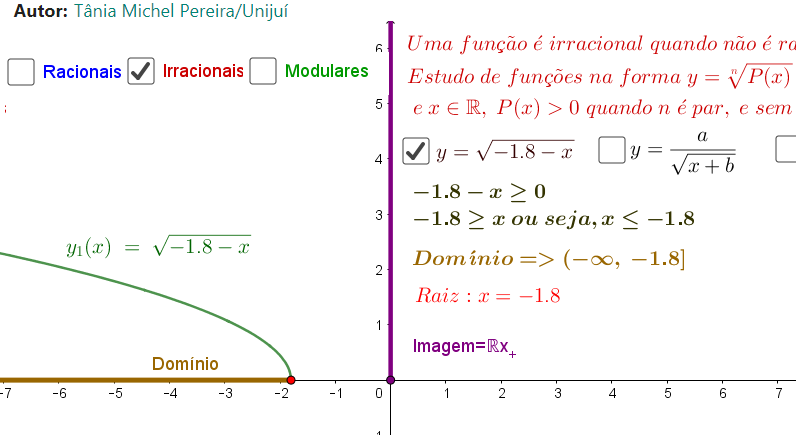
Endereço: https://www.geogebra.org/m/cwfc7ywk
Função Modular
Cada função tem um conjunto da valores que x pode assumir, no caso da função modular na forma y=| ax+c | o domínio é R e este conjunto não é um intervalo limitado, porque a forma intervalar de R é ( -∞, ∞) ou seja de menos infinito a mais infinito.Ja o conjunto dos valores que y e pode assumir é o conjunto dos reais não negativos R+, cujo intervalo é ( 0, ∞) ou seja o intervalo da imagem começa no zero, que é o limite inferior e vai até infinito.
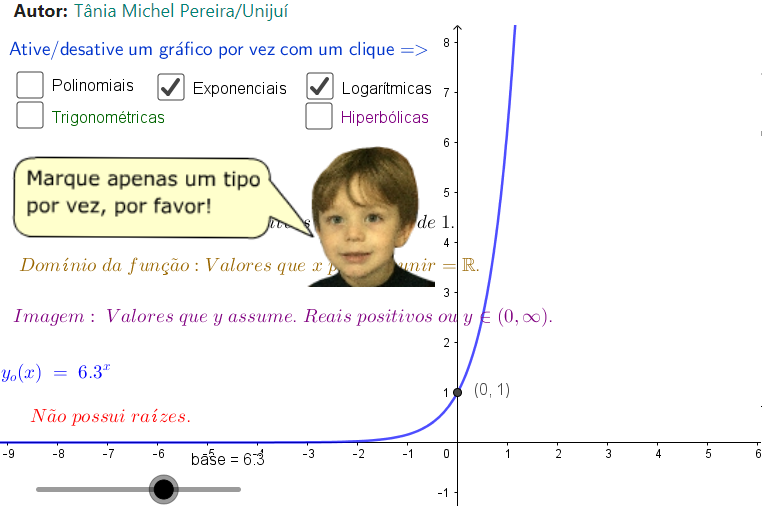
4.2.4 Exponenciais
Para estudar o domínio e imagem e raízes das funções Exponenciais acesse o endereço a seguir e escolha a opção Funções Exponenciais.

https://www.geogebra.org/m/avbzk5q3
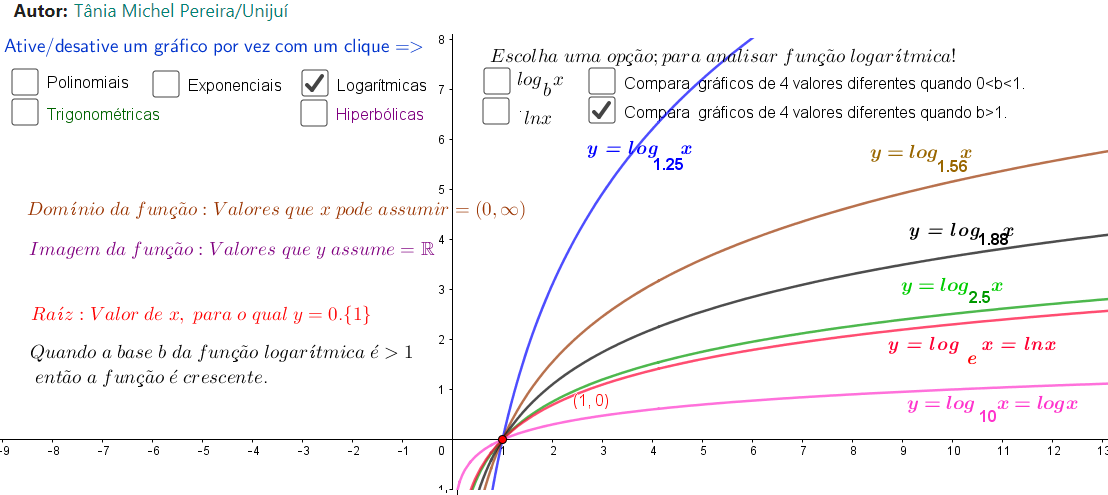
4.2.5 Logarítmicas
Para estudar o domínio e imagem e raízes das funções Logarítmicas acesse o endereço a seguir e escolha a opção Funções Logarítmicas.
4.2.6 Funções Trigonométricas
Acesse os gráficos das funções trigonométricas no plano cartesiano xy.
Para cada uma das funções trigonométricas que aparecem nas opçoes,veja qual é o domínio e imagem no aplicativo do endereço a seguir. Faça anotações sobre intervalos de crescimento e decrescimento, bem como o domínio e imagem, no cadeno da undade.
https://www.geogebra.org/m/t5gkxhze
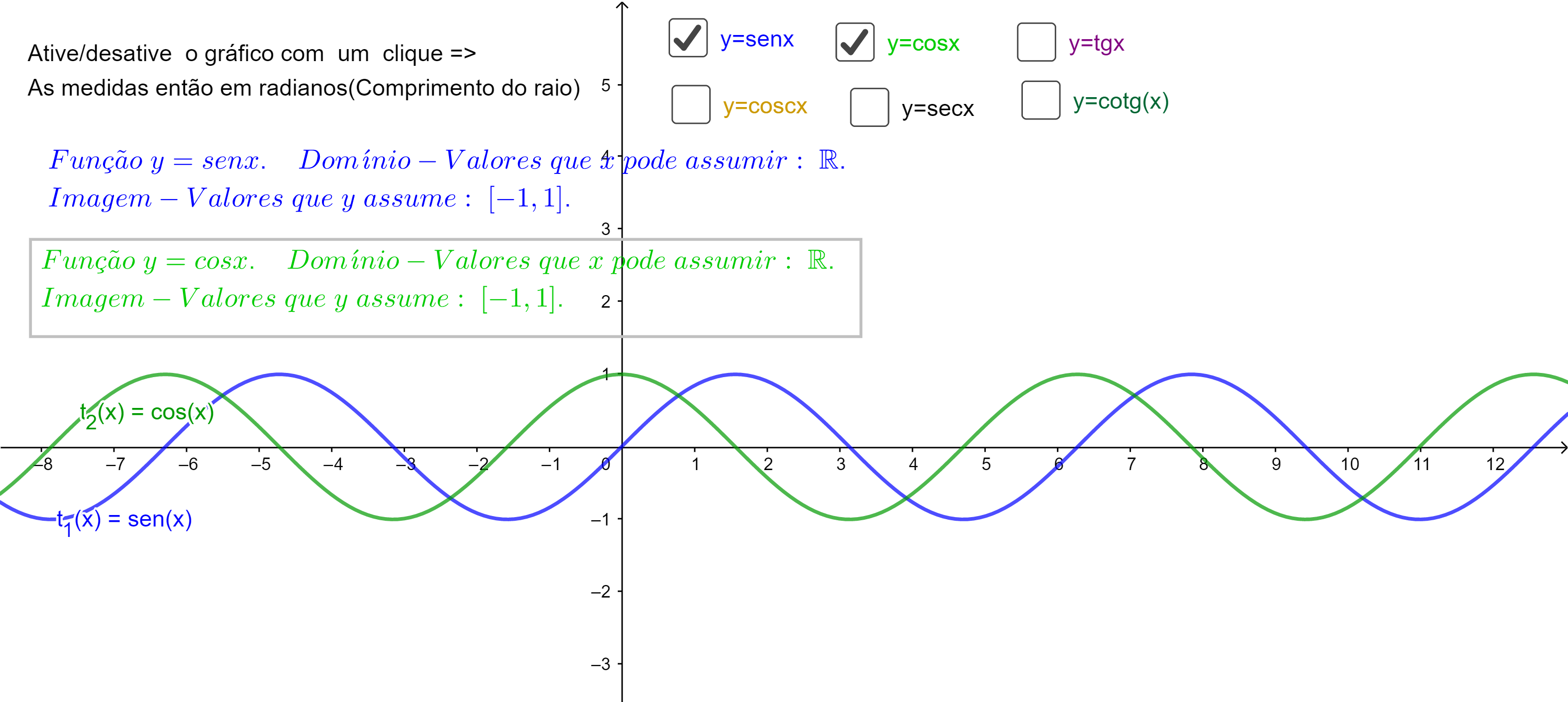
Veja também funções trigonométricas compostas no aplicativo a seguir, escolha a opção trigonométricas e explore um caso de cada vez.
4.2.7 Funções hiperbólicas

Acesse o objeto de aprendizagem do endereço a seguir para explorar as funções hiperbólicas.
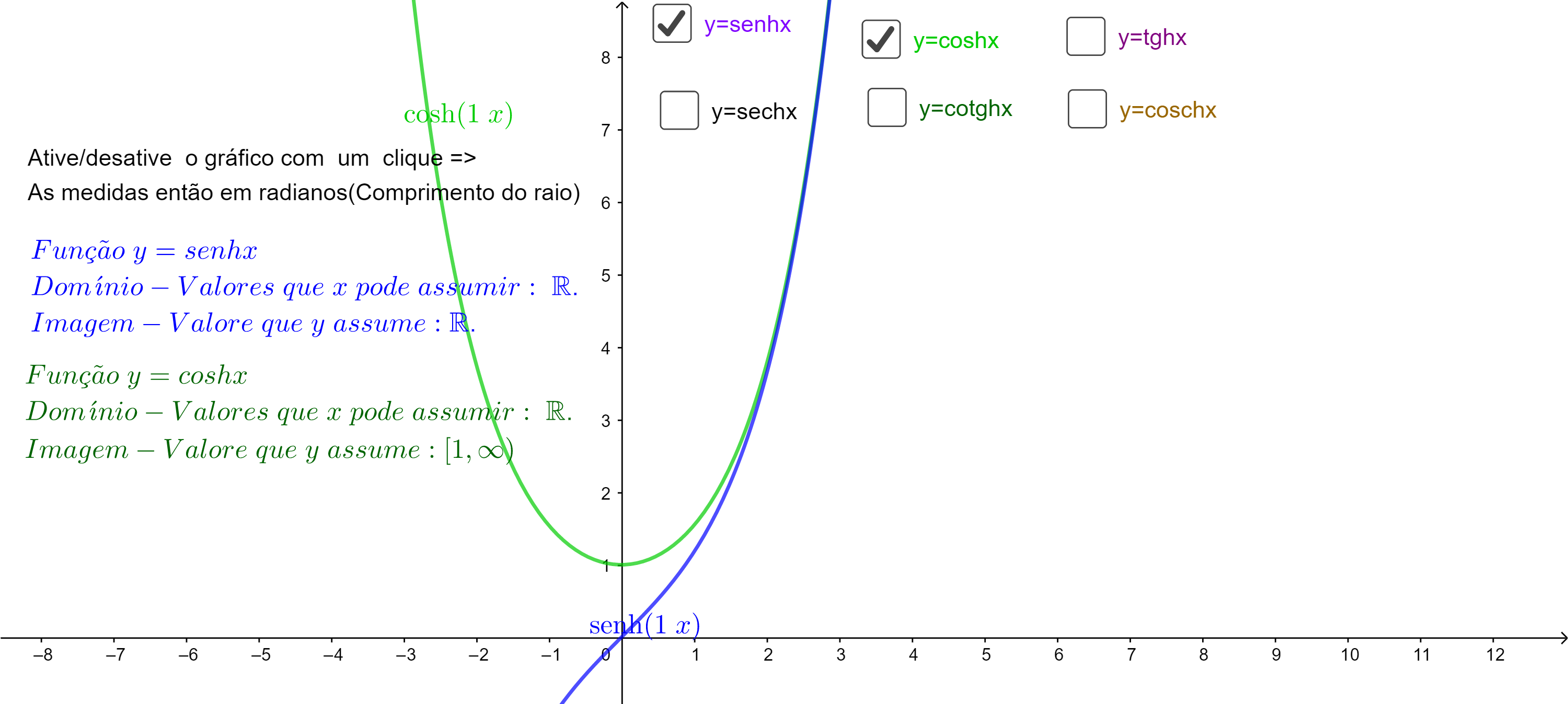
Endereço: https://www.geogebra.org/m/ujvfswxh
Saiba mais sobre trigonometria hiperbólica
A trigonometria hiperbólica, as relações trigonométricas são baseadas nos pontos da parte direita da hipérbole unitário com centro na origem cuja equação que a define é y²-x²=1 onde seu centro é a origem de um plano cartesiano em que cada ponto(x,y) da hipérbole unitária corresponde a (cosh(a), senh(a)) para algum a.
Acesse o objeto de aprendizagem do endereço abaixo para ver a representação geométrica do seno,cosseno e tangente da trigonometria hipebólica. Secante, cossecante e cotangente na trugonometria hiperbólica foram definidas a partir a partir do seno, cosseno e tangente.

https://www.geogebra.org/m/ujvfswxh
https://www.alfaconnection.pro.br/matematica/funcoes/funcoes-hiperbolicas/origem-das-funcoes-hiperbolicas/