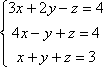
Resolver
o sistema utilizando
o excel baseado
na forma matricial
do sistema AX=B
=> X=A-1B , onde A é a matriz dos coeficientes das variáveis
do sistema e B é a Matriz coluna dos termos independentes, e A-1
a matriz
inversa de A)
Supondo
que o sistema resultante da interpretação do problema seja o seguinte:
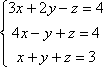
Neste
sistema,
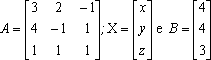 e
e
A-1
terá
que ser calculado, e poderá ser do
conforme 1) e 2) dos passos para encontrar a matriz coluna
X que aparece a seguir:
1)
Marcar uma região para uma matriz 3x4 e digitar os coeficientes do sistema
bem como os termos independentes
2)Marcar
uma região 3x3 para colocar a matriz inversa e digitar ali, diretamente =matriz.inverso()
, e sem acionar enter, posicione o cursor dentro dos
parênteses, e
com ajuda do mouse selecione toda a matriz A , acione as teclas Ctrl
Schift e
acione enter antes de soltar as teclas Ctrl
Schift.
A matriz inversa deverá estar pronta.
3)
Selecione uma região 3X1
para que sejam colocados ali os valores de x, y e z
e sem sair da região digite =matriz.mult()
e sem sair
da região entre
com o mouse dentro dos parênteses
e selecione toda a matriz inversa coloque em seguida ;
(ponto e vírgula).
ainda dentro do parênteses e selecione com o mouse a matriz coluna B,
acione as teclas Ctrl
Schift e
acione enter antes de soltar as teclas Ctrl
Schift.
Os valores
de x, y e z deverão aparecer neste local.
Obs.: Para resolver outros sistemas basta substituir a matriz dos coeficientes e dos termos independentes por cima da matriz do sistema anterior, e tudo se adaptará de forma automática.
Clique aqui para ver planilha do Excel com o exemplo acima resolvido e que pode ser utilizado para resolver sistemas com 3, 4 ou 5 variáveis.