1 – Os números reais

Inicialmente você vai rever o conjunto numérico dos números reais e seus os conjuntos numéricos que o compõe e as principais propriedades.

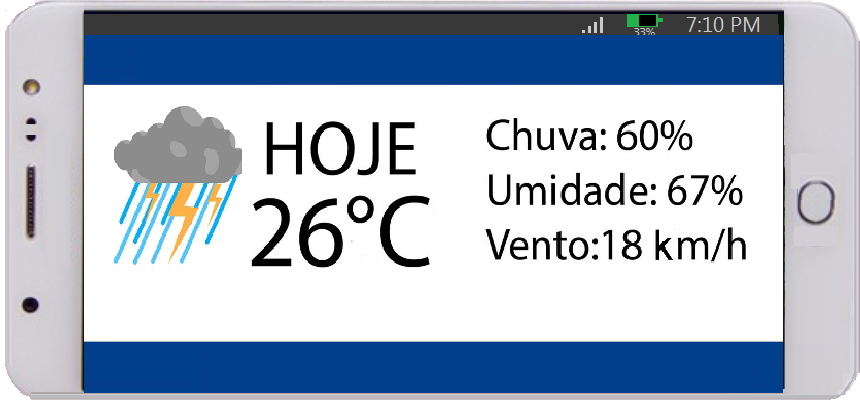
São os números que pertencem ao conjunto dos reais (R) que você utiliza para quantificar características das coisas que fazem parte da nossa vida. Seja ver a carga da bateria celular, a previsão do tempo, o tempo que falta para acabar a aula, iniciar um jogo, saída do ônibus e, principalmente nos estudos que vão preparar você para ser um engenheiro.

Na imagem a seguir são mostrados alguns números reais numa reta numerada.

1.1 Os números reais

Os números reais são formados pela união (È) do conjunto do números racionais Q  com o conjunto dos números irracionais. A representação destes aparece a seguir.

Os números irracionais são aqueles números reais que não podem ser representados na forma p/q onde p e q são inteiros e q≠0. Numa reta numérica estes números são pontos que não fecham uma reta.

Nas calculadoras científicas os números irracionais são mostras com um número limitado de casas decimais. Na figura abaixo aparece o valor aproximado do pnuma calculadora científica virtual.

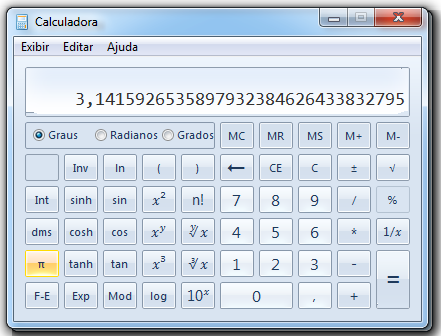
O Valor de p que é utilizado na medida de arcos e em medidas de comprimento, área e volume de objetos, a exemplo da bola de futebol ou estruturas que envolvem formar arredondadas, como é o caso do estádio de Samara, onde ocorreu o jogo do Brasil e México, nas oitavas de final da copa da Rússia 2018.

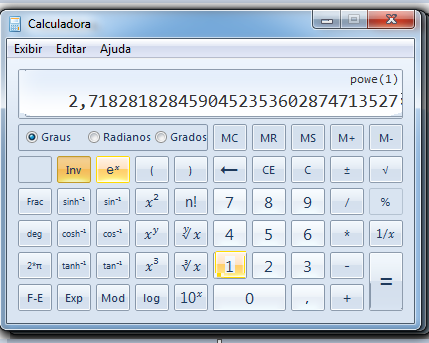
O número e, que vale aproximadamente 2,718, é utilizado como base do logaritmo neperiano e na definição de funções trigonométricas hiperbólicas bem como na representações de números complexos, que não serão explorados nesta disciplina.

1.3 Os números reais racionais

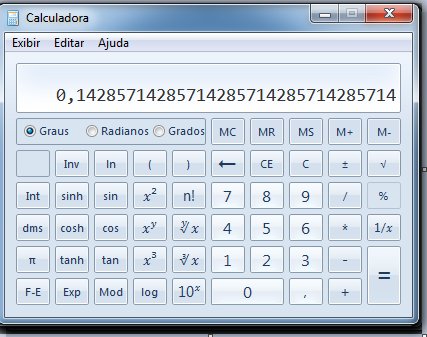
Ao conjunto dos números racionais pertencem todos os números que podem ser representados na forma p/q onde p e q são inteiros, porém q≠0. Ou seja, inclui todos os inteiros, os números fracionários e todos que podem ser representam decimais exatos ou periódicos.
Na figura abaixo podemos ver um decimal aproximado de 1/7, que é um número racional. O decimal correspondente é um decimal periódico, onde o período é 142857.

1.4 Os números reais inteiros

Os inteiros representados sobre uma reta orientada, são pontos isolados na reta com uma distância constante.

Os Números naturais são os inteiros positivos e o zero.

Direcionar para atividades??????????????

1.5  Propriedades dos números reais

1.5.1 Propriedades que envolvem números negativos

Nos quadros a seguir, considere a e b números reais positivos e diferentes de zero e n m nº racional.

1.5.2  Propriedades que envolvem potências

Nos quadros a seguir, considere a e b ;números reais positivos e diferentes de zero, n e m números naturais.

1.5.3  Propriedades que envolvem a radiciação
O que significa radiciação? Radiciação indica que  onde n é um número inteiro diferente maior que zero.

Identificação	Propriedades	Exemplo
1
2
3
4
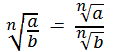5
6		.
7

Quando o denominador de uma fração envolve radicais, o processo pelo qual se transforma essa fração neutra cujo denominador não tem radicais chama-se racionalização de denominadores.
Exemplos:

1.5.4  Propriedades que envolvem o zero

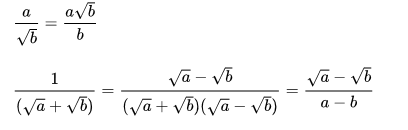
No quadro a seguir, considere o número representado por a, um número real positivo diferentes de zero. O número representado por n é um números natural.

2. Frações ordinárias

Nesta seção você vai rever as operações que envolvem frações ordinárias. Estas são apresentadas na forma a/b onde a e b são números inteiros, com b≠0.  O nome dos termos da fração depende da sua posição:

 Se você precisa saber quanto é 2/3 de R$ 1000,00, então divida o total pelo denominador e multiplique o resultado por 2. Use as regras de arredondamento. Veja anexos II.

Quando vemos a representação 2/3 sem contexto, podemos considerar que se trata de uma divisão de duas unidades em 3 partes e o resultado disto será exatamente dois terços 2/3. Ou seja, 2÷3= 2/3

.

2.1  Frações equivalentes

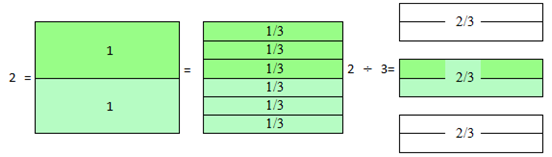
Quando você multiplica ou divide os termos de uma fração por um mesmo número natural, diferente de zero, obtemos uma fração equivalente à fração inicial, ou seja, seu decimal correspondente é o mesmo.
Por exemplo, as frações abaixo são todas equivalentes entre si:

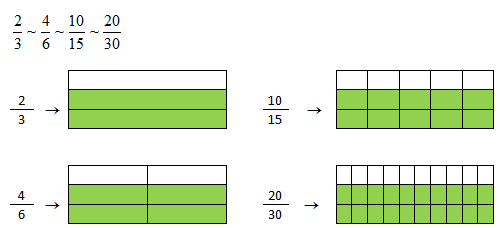
Simplificar uma fração é dividir seus termos por um mesmo número diferente de zero e obter termos menores que os iniciais.
Por exemplo, simplificando a fração 10/15 obtemos a fração 2/3.
Quando simplificamos uma fração e obtemos uma nova fração que não pode ser simplificada, dizemos que foi obtida a forma irredutível da fração dada.
Por exemplo, simplificando a fração 20/30 obtemos a fração 2/3, que está na sua forma irredutível, pois não é possível encontrar simplificar mais.

2.2 Operações com frações

2.2.1  Adição e subtração de frações com denominadores iguais

A soma de frações com denominadores iguais é uma fração cujo denominador é igual ao das parcelas e cujo numerador é a soma dos denominadores das parcelas, ou seja:

Exemplo: se a=2, b=5 e c=1 temos:

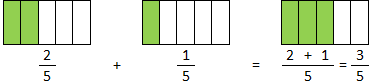
A diferença de duas frações com denominadores iguais é uma fração cujo denominador é igual ao das frações dadas e cujo numerador é a diferença dos denominadores. Isto é:
 

Exemplo: se a=4, b=5 e c=3 temos:

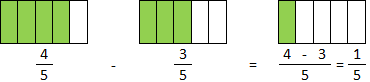
2.3.2  Adição e subtração de frações com denominadores diferentes

Quando vamos somar ou subtrair frações com denominadores diferentes você primeiro reduzi-las ao mesmo denominador e, em seguida, aplicar as regras anteriores.  Dadas as frações .

Na adição temos  onde b.d é, evidentemente um múltiplo comum de b e d, bastando assim transformar as parcelas para frações equivalentes com um denominador comum e no final, basta simplificar no resultado.

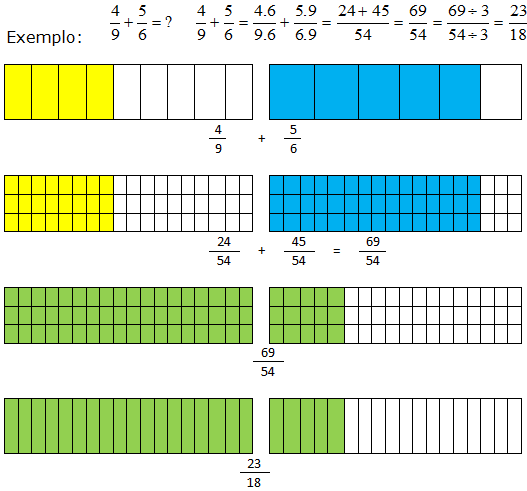
Com a utilização o mmc de 9 e 6 ou mmc(6, 9) que é 18 temos um caminho mais curto.

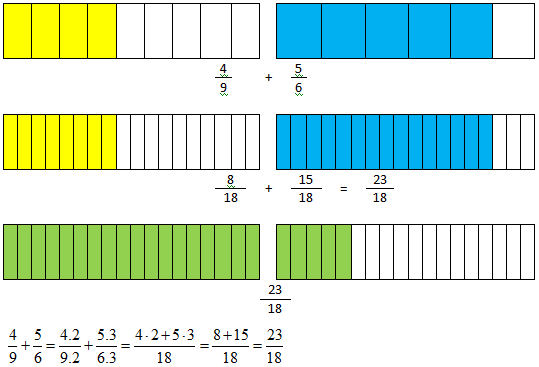
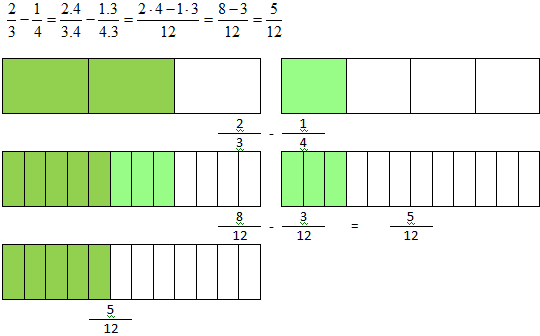
Na subtração temos procede-se exatamente do mesmo modo. Considere o seguinte cálculo: 2/3 - 1/4.  Se você não tiver um aplicativo a sua disposição para efetuar este cálculo e além disto não seja conveniente transformar as frações para números decimais aproximados, sugerimos os seguintes procedimentos: o primeiro passo é reduzir as frações ao mesmo denominador. Para isso você pode encontrar o mmc(3, 4) que é 12, ou utilize como múltiplo comum, o produto dos denominadores. No final você simplifica, se for o caso.  O desenvolvimento fica do seguinte modo:

2.2.2 Multiplicação e divisão de frações

Multiplicação

O produto de duas frações é uma fração onde o numerador é o produto dos numeradores e o denominador é o produto dos denominadores das frações dadas.

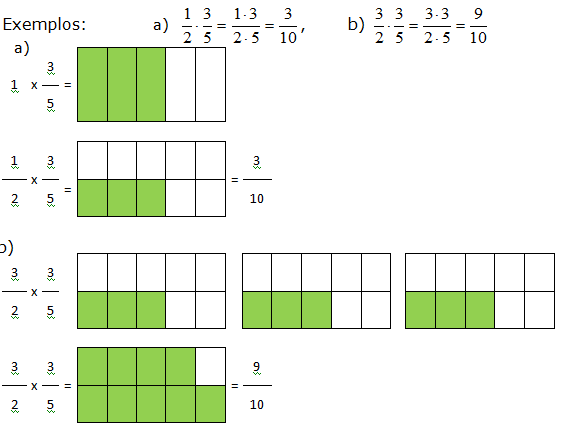
Após a obtenção do produto das frações, devemos simplificar a fração obtida, colocando-a na forma irredutível. Ou cancelar os fatores comuns aos numeradores e aos denominadores antes de fazer a multiplicação, se for o caso.

Divisão

A divisão de uma fração por outra é igual ao produto da primeira fração pelo inverso da segunda. Veja os exemplos.
-Repartir 3/5  entre 3, qual a parte de cada um? 
-Cálculos:  (3/5) : 3  ou   (3/5) x (1/3)     .
Veja uma representação geométrica desta situação:

3 Intervalos de número reais: representação e operações

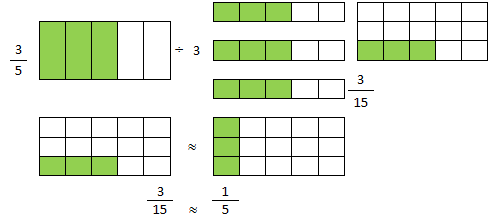
Exercícios com operações de intervalos.
1-Encontre AB,  AB e    A-B  para cada um dos casos abaixo:

a)A = [ -2,  6]  e B = [-1,  4 )                  b)A = [-1,  4)   e  B = [-2, 6 ]
c)A = [ -2,  6]  e  B = (-3,  7 )                 d)A = ( -3,  7)  e B = [-2, 6 ]
e)A = (- ,5  e  B = ( 4, ]             f)A = [ -6,  3]  e B = [2, 4 ]    
 
2-Responda as questões a seguir justificando a resposta.
a)  AB é sempre igual a  B A para qualquer que seja A e B? 
b) AB é sempre igual a   B A para qualquer que seja A e B?
c) A - B  é sempre igual a B - A  para qualquer que seja A e B?

Anexo I

Principais Símbolos utilizados

Alguns símbolos utilizados no curso e que podem ser encontrados na opção Inserir Símbolo no editor de textos.

Critérios de arredondamento.

1-Se o primeiro valor após os que irão permanecer for menor que 5, então apenas elimine as demais casas decimais que estão a sua direita.
Por exemplo: 24,37201 se for arredondado para duas casas decimais fica 24,37.

2-Se o primeiro valor após os que irão permanecer for maior que 5, então o último que permanece fica acrescido de uma unidade.
Por exemplo: 24,37601 se for arredondado para duas casas decimais fica 24,38.

3-Se o primeiro valor após os que irão permanecer for igual a 5, e após este tiverem outros algarismos onde pelo menos um é diferente de zero, então o último que permanece fica acrescido de uma unidade. Por exemplo: 24,37501 fica 24,38.

4-Se o primeiro valor após os que irão permanecer for igual a 5, e após este não tiverem outros algarismos diferente de zero, então o último que permanece fica acrescido de uma unidade somente se o que permanecer é impar, caso contrário o último que fica permanece sem alteração. Por exemplo: 24,37500 fica 24,38 porque o 7 é impar e 24,32500 fica 24,32 porque o 2 é par.