


|
 |

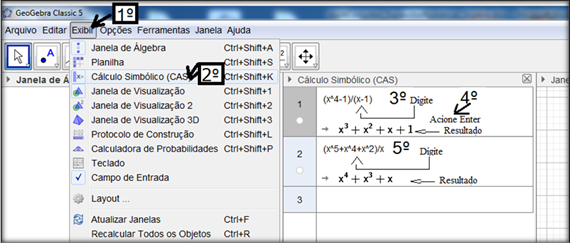
Multiplicação de polinômios com o aplicativo Geogebra
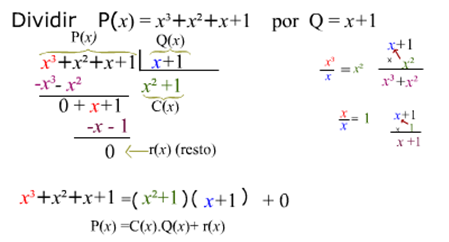
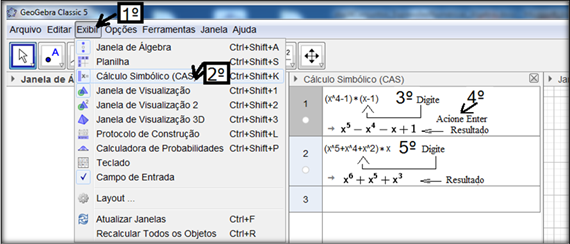
Divisão de polinômios com o aplicativo Geogebra
Nesta seção serão tratados a fatoração e a simplificação de polinômios e expressões. Aos casos abordados são fatoração por: fator comum; agrupamento; trinômio quadrado perfeito; diferença de dois quadrados; diferença de dois cubos e soma de dois cubos.Além disto, será mostrado um exemplo sendo resolvido no aplicativo Geogebra.
As fatoraçãoes e simplificaçãoes algébricas são muito utilizadas nas disciplinas de Cálculo I e II que compõe a grade curricular dos cursos de engenharia. Não são todas as expressões algébricas e/ou polinômios que podem ser fatorados em fatores inteiros ou racionais. Inicialmente serão apresentados alguns casos de fatoração, bem como o modo de obter um resultado utilizando o software Geogebra.
Se um polinômio possui um ou mais fator(es) repetido(s) em cada um dos termos, então coloca-se este(s) em evidência:
Exemplo
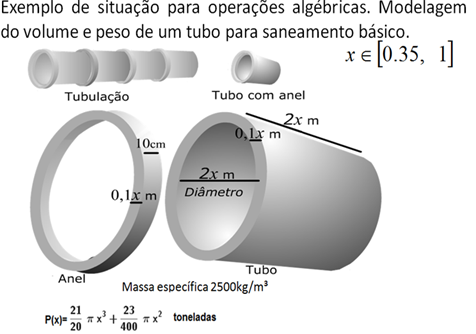
Na expressão do polinômio que expressa o peso de um tubo em função da medida variável x, observa-se que em cada termo pode-se isolar πx². Veja:

A expressão dada e os três resultados representados acima são polinômios equivalentes, ou seja, produzem o mesmo valor numérico quando a variável x assumir um valor específico para um determinado tubo a ser fabricado.
Abaixo aparece a digitação e o resultado da fatoração 3 utilizando aplicativo Geogebra e digitando a primeira linha, obtém-se o resultado da fatoração após acionar a tecla Enter no computador.
Observação: O modelo acima foi construído a partir de fórmula do cilindro. Caso queiras acessar mais fórmulas de figuras espaciais
Na figura a seguir você pode ver 12 peças de vidro colorido para formar um vitrõ único. As dimensões são dadas em decímetros e fixadas no momento do corte.
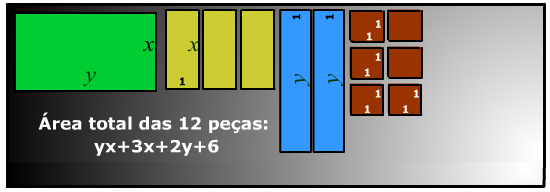
Quando um polinômio ou expressão algébrica possui duas ou mais variáveis com fator(es) repetido(s) em parte dos termos, então pode-se tentar a fatoração em duas ou mais etapas. Veja o caso da figura a seguir.
xy + 3x + 2y + 6
Nos dois primeiros termos da expressão, podemos colocar y em evidência e nos seguintes o número 2 pode ser colocado em evidência, Veja como fica:
x(y + 3) + 2(y + 3)
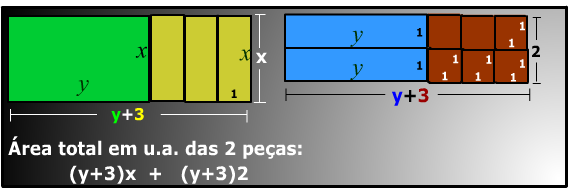
Na expressão resultante possui, o fator comum y + 3 pode ser colocado em evidência e termos a expressão a seguir.
(y + 3)(x + 2)
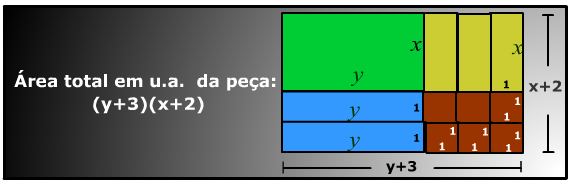
No aplicativo Geogebra você deve digitar o que aparece imagem a seguir:
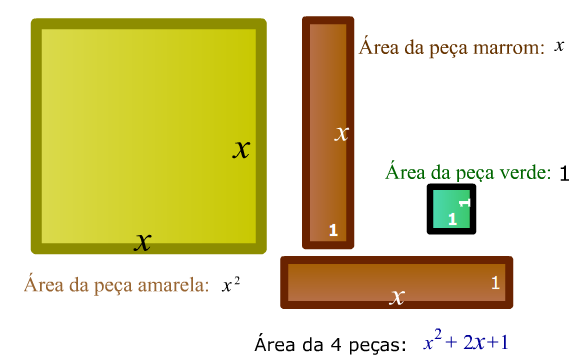
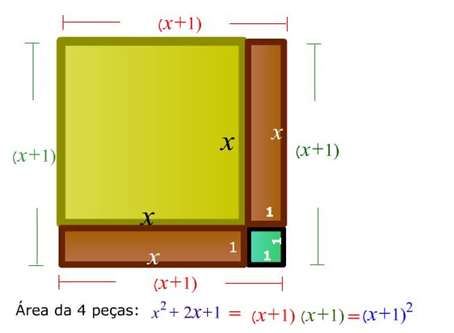
Se um trinômio for resultante de quadrado de um binômio, então basta substituir o trinômio por este. Veja:
P(x) = x² + 2x + 1
A diferença de dois quadrados resulta do produto de uma soma de dois termos pela diferença destes mesmos termos. Portanto a sua fatoração é o produto da soma pela diferença da raiz quadrada de cada um dos termos.
Outros exemplos que podem auxiliar em simplificaçãoes:
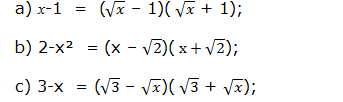
Ao utilizar o Geogebra, digitando a primeira linha, obtém-se o resultado da fatoração após acionar a tecla Enter no computador.
Quando um polinômio tiver um formato de soma de dois termos elevado ao cubo (a³+b³), este poderá ser fatorado assim:
a³ + b³ = (a + b)(a² – ab + b²)
Exemplo: x³ +1=(x+1)(x² – x + 1)
Quando um polinômio tiver um formato de diferença de dois termos elevado ao cubo (a³ - b³), este poderá ser fatorado conforme segue:
a³ - b³ = (a - b)(a² + ab + b²)
Exemplo: x³ -1=(x+1)(x² + x + 1)
Utilizando o Geogebra temos
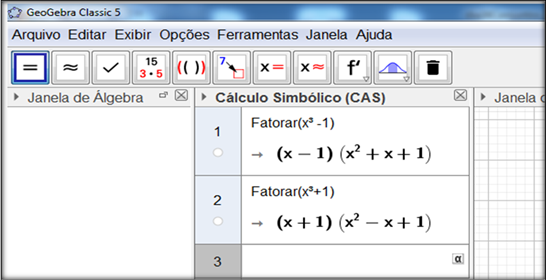
Exercícios evolvendo polinômios
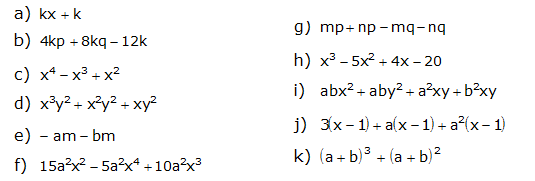
2. Fatore os trinômios abaixo.
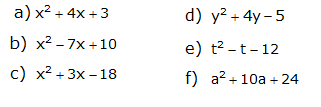
Gabarito dos dois exercícios acima
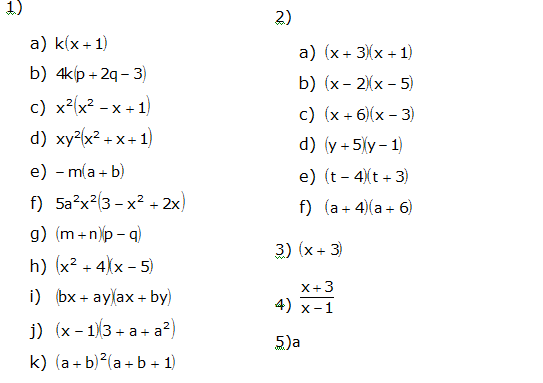

5) Análise as afirmativas a seguir e marque a alternativa correta com relação a veracidade destas considerando as medidas das peças da figura a seguir
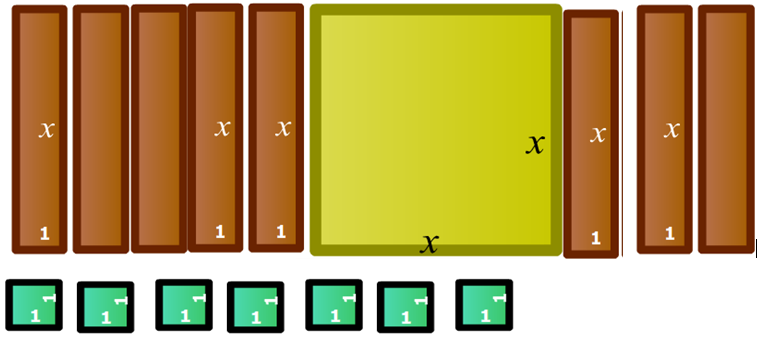
Observação: considere que as peças, da figura acima, podem ser deslocadas e giradas, mas não podem ser cortadas.
I - Para formar um quadrado com as peças acima apresentadas é necessário adicionar mais 9 quadrados com uma unidade de área. Após isto, a área total das peças soltas será x² + 8x + 16 unidades de área. A expressão que representa o cálculo da área de um quadrado, a partir da medida do lado, é (x+4)² unidades de área.
II – A área total das peças soltas e visíveis na figura apresentada, é x² + 8x + 7. É possível formar um retângulo, com as peças. A base e a altura podem ser (x+1) e (x+7).
III - Para formar um quadrado com as peças acima apresentadas é necessário adicionar mais 3 quadrados com uma unidade de área. A área total das peças soltas será de x² + 8x + 10 unidades de área e a expressão que representa o cálculo da área de um quadrado, após adicionar 3 unidades de área 1 é (x+1)(x+10) unidades de área.
IV - A área total das peças apresentadas na figura é x² + 10x + 25 unidades de área e a expressão que representa o cálculo da área de um quadrado é (x+5)(x+5) unidades de área.
V - A área total das peças apresentadas na figura é x² + 10x + 1 unidades de área e a expressão que representa o cálculo da área de um quadrado é (x+3)(x+3) unidades de área, após acrescentadas mais 8 peças de uma unidade de área.
São verdadeiras apenas:
a) I e II. (resposta correta)
b) I, II e III.
c) I e IV.
d) I, II e V.
e) II, III e IV.
Exercícios que envolvem operações com polinômios
Considere os seguintes polinômios para as questões seguintes.
P = x4 + 5x3 +6x2 + x - 1; Q = x +2; H = x5 + 7x4 +16x3 + 13x2 + x - 2
L = x4 + 4x3 +6x2 + x + 1; J = x3 +6x2 + 3x + 1; I = x+1 e S= x2- 4.
Obtenha o resultado de:
| a) P+Q | e) L/I² | i) J / I |
| b) P . Q | f) L/ J | J) H / I (cociente e resto) |
| c) P / Q | g) I³ | l) P/S (cociente e resto) |
| d) H / P | h) S . I | m)Q . S |