8-Operações entre Matrizes
8.1 Adição, Subtração e multiplicação
Se A e B são matrizes definidas no programa e de mesma ordem, A+B e A-B A*B indicam respectivamente a matriz soma, matriz diferença, e matriz produto. Pode-se fazer o produto de duas matrizes de ordens diferentes desde que o número de colunas da primeira matriz seja igual ao número de linhas da segunda matriz.
Exemplos:
>>k=8
>>A=[1 0 3 1; 2 1 3 1; 1 7 2 1;1 2 1 2 ]
>>B=[1 1 1 1; 2 2 2 2; 4 4 4 4; 3 3 3 3]
>>A+B
>>A-B
>>A*B
>>A+k
>> A=[ 1 2 3 ; 2 5 6 ];
>> B=[ 3 1 ; 3 3 ; 4 9 ];
>> A*B
8. 2 Significado Divisão / e \
definida pelo MatLab
Se A uma matriz quadrada e não singular e B de dimensões compatíveis em cada caso. Então,
X = A \ B = A-1 B = inv(A) * B
X = B / A = B A-1 = B * inv(A)
Se A não for quadrada, o resultado X é obtido como solução de
A x X = B ou X x A = B no sentido de mínimos quadrados.
Obs. B / A = (A' \ B' )'
8.3 Potenciação ^
Seja A uma matriz quadrada e p um escalar. Então,
A ^ p = Ap se p for inteiro
A ^ p = V*A* D^p * V-1 , [V,D] = eig(A) para p qualquer
No caso em que A é um escalar e P uma matriz quadrada, a função de matriz A^P (cujo resultado é uma matriz de mesma dimensão de P) é calculada através dos autovetores e autovalores de P.
Obs. X^P , X e P matrizes, não é definido.
8.4 Operações entre os elementos de mesma posição, para matrizes de mesma ordem
É possível encontrar uma matriz Cmxn que é formada pelo elementos que resultam de alguma operação entre os elementos da mesma posição, ou seja, cij =aij (operação) bij, . Para obter uma matriz desta forma o sinal da operação desejada é antecedida por um ponto, ou seja,
A . (operação) B
onde, no lugar de (operação) deverá ter :
1. A.*B para multiplicação,
2. A./B para divisão à direita,
3. A.\B para divisão à esquerda
4. A.^n para potenciação
Exemplo:
Digitando-se
>>
A=[
1 2 3 ; 2
5 6 ]
Aparecerá
A =
1 2 3
2 5 6
Exemplo:
Digitando-se
>>
B=[ 2
3 0 ; 9
1 4 ]
aparecerá
B =
2 3 0
9 1 4
Digitando-se
>> C= A+B
aparecerá
C =
3 5 3
11 6 10
Digitando-se
>>
C= A . * B
aparecerá
C =
2 6 0
18 5 24
Digitando-se
>> C=
A . / B
aparecerá
C=
0.5000 0.6667 Inf
0.2222 5.0000 1.5000
Digitando-se:
a) C= A .\ B aparecerá C= 2.0000 1.5000 0
4.5000 0.2000 0.6667
b) C= A .^ B o resultado é C= 1 8 1
512 5 1296
8.5 Exercícios envolvendo operações com matrizes
Dadas as matrizes
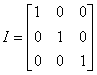 ;
;
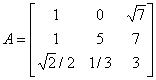 ;
;
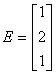
D [ 1 2 3 ]
i)Efetuar as seguintes operações utilizando o MatLab
Obs.: algumas operações dos exercícios são impossíveis, e neste caso terá que ser dado o motivo de operação ser impossível.
1) A2;
2)BxA; 3)AxB;
4)B2; 5) D2; 6)E2 ;
7) DxE; 8) ExD; 9)A-1B;
10) B-1 A; 11)A+B; 12) A-B; 13) D+E;
ii)Encontrar o valor da matriz F para cada caso:
1) fij=aij.bij; 2) fij=aij/bij; 3) fij=bij/aij; 4) fij=aijbij; 5) fij= bijaij;