Atividades de revisão e complementação de alguns conteúdos de matemática do Ensino Fundamental e Médio, utilizando o computador
As atividades a seguir envolvem alguns conteúdos do ensino fundamental e médio.
Operações algébricos básicas no Maple
·
o sinal + indica adição;
·
o sinal
- indica subtração;
·
o sinal ^
ou ** indica
potenciação;
·
o sinal *
indica multiplicação ;
·
o sinal
/ indica divisão ;
·
para indicar
radicais é utilizado o expoente fracionário.
Desenvolva
as tarefas utilizando o programa Maple:
1)Encontre
o resultado em forma de fração ordinária ,
número misto e decimal aproximado:
![]() =
=
![]()
![]()
![]()
Para
encontrar o resultado da última digita-se
a:=(2/3)/(1/5) ;
Obs.: Após a digitação de cada
instrução, é
necessário colocar ; (ponto e vírgula) e
acionar Enter caso se queira
visualizar o resultado. Caso não
se queira visualizar o resultado é necessário colocar :
(
dois pontos) e acionar Enter.
Para
ver a parte inteira, a
parte fracionária e o decimal aproximado
do último resultado, ao mesmo tempo digita-se:
floor(a),
frac(a),
evalf(a) ;
Obs.: Áspas podem ser
utilizadas para substituir a digitação do último resultado
obtido.
Utilize
a calculadora para encontrar o resultados do último cálculo da questão 1)
Para
traduzir estes comandos para outros “apelidos”
que se queira dar aos comandos pode-se
digitar o que segue.
alias(parteinteira=floor, partefracionaria=frac, decimal=evalf);
(2/3)/(1/5);
parteinteira(“) ,
partefracionaria(“) ,
decimal(“);
2)
Se 39874
bolitas forem
repartidas 798 crianças,
quantas bolitas receberia cada criança e quantas bolitas sobrariam?
Para
encontrar o quociente e o resto digita-se:
iquo(39874 , 798);
irem(39874 , 798);
alias(restoi=irem, quocientei=iquo);
## fazendo a tradução
recebem:=quocientei
(39874 ,
798) ;
sobram:=
restoi(39874 , 798);
Resolva
o problema 2 com a calculadora utilizando
somente
a)
a operação subtração;
b)
as operação
adição e subtração ;
b)divisão, multiplicação e
subtração;
3)Encontre
o resultado de cada uma das expressões:
![]()
 .
.
Obs: Utiliza-se somente parênteses
para fazer agrupamento no Maple.
Para
obter o resultado da última expressão,
digita-se:
( 5^(-3) - (
4/8^(1/3)-6*( 35- 7/5 )
) -10);
evalf( ",
6);
# para obter o resultado na forma de decimal com 6 algarismos
significativos
Utilize
a calculadora para encontrar o resultado
da última expressão da questão 3
4)
Represente cada um dos números
pelo produto de seus fatores primos e depois marque os números primos
ou seja,
os que não podem ser
representados por um produto de outros números inteiros.
a) 32 b)
81
c)243
d)29
e)17 f)2
g)23
h)252 i)257
j)99.
Para
encontrar a representação do último
digita-se:
ifactor(
99);
# ou traduzindo ifactor
para fatorespri
alias( fatorespri =
ifactor );
fatorespri(99);
5)Encontre
os divisores dos números da questão anterior e verifique o número de
divisores dos números que foram marcados
na questão anterior por serem primos. Existe algo em comum?
Para
encontrar o conjunto dos divisores do penúltimo digita-se:
with(numtheory): # para
ativar pacote da teoria
dos números
divisors(
257);
# traduzindo
alias( divisores = divisors
);
divisores(257);
6)Encontre
o termo desconhecido :
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
A
primeira e última questão estão
resolvidos a seguir:
solve( x/69=23/13,
x);
alias(resolva=solve); ## traduzindo o comando
resolva( (x/4)
/ 3 =
2 / (3/7), x);
7)Fatore
as expressões
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
Para
encontrar o resultado da fatoração das duas últimas,
pode-se digitar:
factor(x^5+1);
alias(fatore=factor);
fatore(x^7+1);
8)Encontre
o quociente e o resto da divisões em
seguida verifique se existe
alguma regularidade nas respostas. É
possível fazer alguma
régra?
![]()
![]()
![]()
![]()
![]()
![]()
Para
obter os resultados do ítem c e
d pode-se
digitar:
quo( (x^8+1), (x+1),
x); rem(
(x^8+1),
(x+1), x);
alias(quociente=quo,
resto= rem);
quociente( (x^8+1), (x-1),
x); resto( (x^8+1), (x-1),
x);
9)
Faça o desenvolvimento das potências a seguir e descreva as regularidades que podem
ser percebidas
![]()
Para
obter o desenvolvimento da última digita-se
expand( (a+b)^3
);
10)Simplifique
as expressões
![]() ;
;
![]() ;
;
![]() .
.
Para
simplificar a última digita-se
simplify(
x*y*z/(a*z*y)
) ;
normal(
x*y*z/(a*z*y) ) ;
11)Resolva
as equações algébricas
![]()
![]()
![]()
![]()
![]()
Para
resolver as últimas digita-se
solve(x^5-6*x^4-5*x^3+2*x^2-x+7
, x );
allvalues(");
alias(resolva=solve, valores=allvalues);
resolva(x^4-5*x^3+2*x^2-x+7 , x );
#valores(“);
12)
Resolva as diversas equações ,
inequações e sistemas
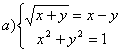 ,
,
![]() ,
,

![]() ,
,
![]() ,
,
![]()
![]()
![]() ;
;
![]()
Para
resolver o sistema do item a) pode-se
digitar
s1:={ (x+y)^(1/2) = x-y ,
x^2+y^2=1 };
solve(s1, {x,y} );
Para
resolver as últimas duas equações pode-se digitar
solve(log[2](x)-log[2](5*x-6),x);
solve(2^(2*x)-2^(x+2)+4=0,
x );
13)Racionalize
os denominadores das seguintes expressões;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]()
Para
racionalizar a primeira e a última
expressão digita-se:
readlib(rationalize):##
racionalização oitava
(x+y)/(x+(3)^(1/2));
rationalize(");
4/3^(1/3);
14
)Converta os números decimais para frações ordinárias:
a)
0,125;
b) 0,3333333333; c) 0,333;
d)1,666666666 ; e)1,666;
f) 0,999999999; g)0,99999.
Os
dois primeiros podem ser obtidos do seguinte
modo:
convert(
0.125, fraction
);
convert(
0.3333333333,
fraction );
convert(
0.3333333333, fraction,
exact
);
convert(0.3333333333, rational);
15)Arredonde
os números decimais para
números inteiros
a)
20,5
b)20,4 c)20,8
d) 12,2 e)12,5
f) 12,9
g)7,2 i) 7,5
j)7,8
Para
arredondar o primeiro valor pode-se digitar o seguinte:
n :=20.5;
trunc(n) ; # despresa todas as casas decimais
floor(n); # arredonda para inteiro
igual ou menor que x,
mais próximo
round(n) ; # arredonda para inteiro
mais próximo
ceil(n); # arredonda para inteiro igual ou maior que
x, mais próximo
16) Faça o gráfico das funções
![]()
![]()
![]()
![]() ;
;
![]() ;
;
![]()
Para
fazer num só plano cartesiano os gráficos
das três primeiras funções pode-se digitar:
with(plots):
# para abrir o pacote gráfico
do Maple e reconhecer comandos
relacionados com gráficos
y1:=x+3;
y2:=x-3;
y3:=x;
plot(
{y1,y2,y3},
x=-10..10);
17.Exemplo de aplicação de resolução de sistemas
1) Um feirante oferece 3 tipos de sacolas com verduras, todas são vendidas a R$ 2,50. A composição das sacolas é o seguinte:
Sacola tipo 1:
2 maços de cenouras, 3 espigas de milho verde e 1 repolho.
Sacola tipo 2:
3 maços de cenouras, 1 espigas de milho verde e 1 repolho.
Sacola tipo 3:
1 maço de cenouras, 2 espigas de milho verde e 2 repolho.
Deseja-se saber a que preço está sendo comercializado, por este feirante , cada maço de cenoura , cada espiga de milho e cada cabeça de repolho?
>e1:=2*c+3*m+r-2.5;
>e2:=3*c+m+r-2.5;
>e3:=c+2*m+2*r-2.5;
>solve({e1=0,e2=0,e3},{c,m,r});
>##ou
>sistema:= { 2*c+3*m+r=2.5, 3*c+m+r=2.5, c+2*m+2*r=2.5 } ;
>
precouni:=solve(sistema, {c,m,r} );
>## ou somente
>solve( { 2*c+3*m+r=2.5, 3*c+m+r=2.5, c+2*m+2*r=2.5} );
18)
Alguns procedimentos
que podem servir como exemplo para estabelecer relações entre conteúdos
## procedimento para comparar medidas de área e perímetro de retângulos
- conteúdo de quinta série
retangul:=proc(n)
local i;
print( ` base, altura,
perímetro,
área `);
for i
to
n-1 do
print(i,
n-i, 2*i+2*(n-i),
i*(n-i) );
od;
end:
### executar o procedimento
anterior
retangul(10);
19)
Uma “malha” ou “loop”
para comparar juros simples e juros compostos variando o número de períodos
-conteúdo de sexta série
c
:= 100; i :=
10;
for t
to 10 do
tempo:=t
,
Js=decimal(c*i*t/100) ,
Jc=decimal(c*(1+i/100)^t -c):
od;