16 Funções para fatoração e decomposição de matrizes
16.1
Fatoração triangular
A fatoração triangular, que transforma uma matriz quadrada Anxn no produto de duas matrizes triangulares Lnxn e Unxn uma triangular superior e outra triangular inferior é denominada fatoração “LU”. Para encontrar estas matrizes triangulares, após definida a matriz A, digita-se [L, U]=lu(A) .
Exemplo
Se A =
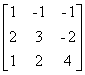, para obter as matrizes triangulares pode-se
digitar
>> [L, U]=lu(A)
o resultado é
L =
0.5000 1.0000 0
1.0000 0 0
0.5000 -0.2000 1.0000
U =
2.0000 3.0000 -2.0000
0 -2.5000 0
0 0 5.0000
Pode-se observar que L é uma matriz
triangular inferior com a primeira
e segunda linha permutada. Fazendo o produto para a verificação se obtém a
matriz A .
» L*U
ans =
1 -1 -1
2 3 -2
17 Decomposição de matrizes retangular
Dada uma matriz Amxn
retangular, encontrar 3 matrizes U,S,V tais que UxSxVT=A, onde Umxm
é uma matriz quadrada de ordem m;
Smxn éuma matriz retangular coma as mesmas dimensões de A
e Vnxn
uma matriz quadrada de osdem n.
» [U,S,V]=svd(A)
U =
-0.2527 0.0489 0.9663
-0.0476 0.9969 -0.0629
0.9664 0.0619 0.2496
S =
4.7231 0 0
0 4.1291 0
0 0 1.2819
V =
0.1309 0.5097 0.8503
0.4325 0.7424 -0.5116
0.8921 -0.4347 0.1232
Fazendo o produto de U e S pela transposta de V obtém-se a matriz A .
>>U*S*V’