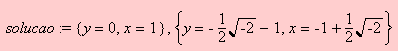8. Resolução de equações, inequações e sistema de equações
Sintaxe:
sistema:={<equação
1>,
<equação 2>, ...,
<equação n>};
solve( sistema, { x1,x2, ... xn } );
## onde x1, x2,
..., xn são as incógnitas.
Seguem alguns exemplos de equações e
sistemas de equações que podem ser resolvidas pelo Maple juntamente com a
sintaxe.
A função que serve para
resolver equações ou sistemas de equações é solve.
A sintaxe para
resolver equações pode
ser :
solve(equação); caso haja
somente uma incógnita e não envolva parâmetros Veja o exemplo,
para resolver a equação
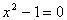 .
.
> solve(x^2-1);
>solve(x^2-1=0);
ou
solve(equação,
incógnita);
que é a forma mais geral
>solve(x^2-1=0 , x
);
> solve(x^2+6*x+9=0,
x );
Para encontrar as fórmulas
para resolver as equações
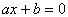 e
e
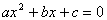 com relação a x
digita-se :
com relação a x
digita-se :
> x
= solve(a*x+b=0,
x ) ;
>solve(a*x^2+b*x+c=0,
x );
Os resultados obtidos são

Para resolver o sistema
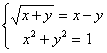 ,
,
digita-se
>
sisxy:={x^2+y^2=1, (x+y)^(1/2) = x-y
}:
>solucao:=solve(sisxy,
{x,y} );
obtém-se
um resultado idêntico a
:
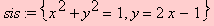
Digita-se
>
sis:={ x^2+y^2=1, y= 2*x-1 };
resulta
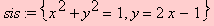
continuando a digitação
>solu:=solve(sis ,{x,y});
resulta
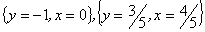
Exemplo 5:
Digitando-se
>s:={2*a-b-8*c+d=0,a+b=1,c+d=3,a+d=7};
aparecerá
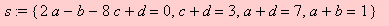
e digitando-se
resulta o conjunto solução:
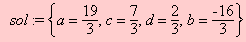
Exemplo 6:
Para resolver a equação
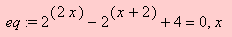
digita-se
>solve(2^(2*x)-2^(x+2)+4=0,
x );
e
o resultado obtido é
1,
1.
Veja várias formas de
obter a solução de equações algébricas:
> p:=x^5-6*x^3-7*x; #
para definir o polinômio
>solve(p=0) ; # mostra as soluções
reais e imaginárias
> fsolve(p=0) ; # mostra as soluções reais;
> isolve(p=0) ; # mostra as
soluções inteiras;
>readlib( realroot ):
# Lê da pasta
“biblioteca” função realroot
>realroot( p,
1); #
Fornece intervalos que contém somente uma raiz real,
os quais tem >################ amplitude igual a
1 (um).
> realroot( p,
1/1000); # intervalos
com aplitude iqual a 1/1000.
De modo semelhante à
resolução de sistemas e equações,
pode-se resolver inequações.
Para resolver
a inequação | x+6 |
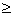 5
digita-se:
5
digita-se:
>solve( abs( x + 6 ) > =5 , x);
e obtém-se como resultado
RealRange(-¥,-11),
RealRange(-1, ¥).
Este
resultado significa que os
valores reais que satisfazem a inequação
pertencem a um dos intervalos
(-¥, -11] ou [-1,
¥).
Para resolver
a inequação | x+6 | > 5
digita-se:
>solve( abs( x + 6 ) > 5 , x);
e obtém-se como resultado
RealRange( -¥,
Open(-11) ),
RealRange( Open(-1) ,
¥ ).
Este
resultado significa que os
valores reais que satisfazem a inequação
pertencem a um dos intervalos abertos
(-¥, -11) ou (-1,
¥).

solve( f >0,x);
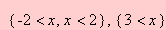
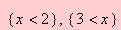
Anterior
Próximo Sumário
Sair
![]() .
.![]() e
e
![]() com relação a x
digita-se :
com relação a x
digita-se :
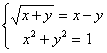 ,
,