


|
 |
Disciplina: Pré-Cálculo
Unidade 2 - Grandezas Proporcionais
2.1. Razão e Proporção
Grandezas proporcionais, aplicações de razão e proporção em diversas situações2.1.1.Razão
Dados dois números a e b, com b0, chama-se razão entre a e b ao quociente indicado por (a:b) ou
.
Nome dos termos: a é 1o termo ou antecedente e b é o 2o termo ou consequente.2.1.1.1. Razão entre grandezas da mesma espécie
A razão de duas grandezas de mesma espécie é o quociente dos números que medem essas grandezas numa mesma unidade.
Exemplo
As soluções A e B são preparadas para desinfetar as mãos, como ação preventiva conta a o coronavírus. A solução A contém 213 litros de água e 47 litros de álcool. A solução B, contém 55 litros de álcool e 258 litros de água. Qual das duas soluções tem maior teor alcóolico?
Seguem diversas aplicações de razão.
Aplicação 1: Escala
Escala em matemática(E) é a razão entre a medida de um comprimento no desenho(d) e a medida correspondente ao comprimento real(D), obtida a partir das medidas expressas na mesma unidade.
A escala, utilizada em desenhos técnicos e mapas, é a razão entre dois números após transformação de medidas para a mesma unidade. Além disto, existem normas técnicas uso e formas de expressão.
Para escala reduzida é utilizada a razão d/D, e para escala ampliada é utilizada a razão inversa.Relação da escala reduzida:
E=\frac{d}{D}Relação da escala ampliada:
\frac{d:d}{D:d} =\frac{1}{E}\; ou\;1:EAcesse o vídeo do endereço a seguir.

https://www.youtube.com/watch?v=NH9b4wn7f4E&feature=youtu.be&t=37Mais aplicações de escala
Fonte:Print do vídeo: https://www.youtube.com/watch?v=D7jUSnZYLbkExemplos de escala ampliada
No desenho técnico peças minúsculas de máquinas, fotos com utilização do recurso macro.
Imagem 1 Imagem 2
Fonte da imagem2: Adaptado a partir de print de tela do vídeo
<https://www.youtube.com/watch?v=C9Nn_wgWNEs >2.1.1.2 Razão entre grandezas de espécies diferentes
A razão de duas grandezas de mesma espécie é o quociente dos números que medem essas grandezas numa mesma unidade.
Aplicação da razão em resistência de materiais
A tensão é definida pela seguinte razão:
Tensão(s) = F/A
A tensão é dado em MPa(N/mm²) onde F é a força(ou carga) aplicada sobre a área inicial A.
Fonte:Elabordo a print de imagens do vídeo do endereço :<http://www.ufjf.br/lrm/files/2009/04/tracao_aco_log.wmv> Acesso em mar. 2019. com adaptações.
Deformação
A deformação é a razão entre a variação(Dl) de comprimento final(lf) e o comprimento inicial(l0).
e =\frac{lf-l0}{l0} \;ou\; \frac{Dl}{l0}\;
Fonte: UNIJUí
Aplicação da razão em medidas de densidade
Densidade demográfica
A densidade demográfica é a razão entre a população total de uma região(P) e a área da região em km2(A)
DP=\frac{P}{A}
Densidade de um corpo Densidade de um corpo: razão entre a massa de um corpo e o seu volume.
https://www.minhaconexao.com.br/ <acesso em 22 mar. 2019>, com .adaptações
Acesse o endereço abaixo para ver mais exemplos sobre razão entre dois valores ou duas grandezas.
https://pt.khanacademy.org/math/pre-algebra/pre-algebra-ratios-rates/pre-algebra-visualize-ratios/v/solving-ratio-problems-with-tables-exercise?modal=1Situação experimental
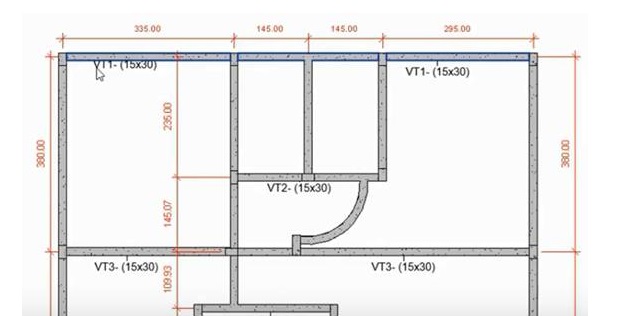
Deseja-se verificar a razão entre a quantidade de etanol e a gasolina comum (mistura de gasolina tipo A com etanol), bem como a razão entre a quantidade de etanol e a gasolina tipo A, ambas vendidas no posto em que foi realizado o experimento?
Seque quadro com os dados experimentais relacionada à imagem acima.
Fonte consultada:
https://duvidasgasolina.hotsitespetrobras.com.br/se-a-petrobras-aumentar-a-producao-de-petroleo-isso-impactara-o-preco-da-gasolina/
http://www.anp.gov.br/images/QUALIDADE/BOLETIM/BQ_COMBUSTIVEIS_032018.pdfO vídeo a seguir apresenta um exemplo que envolve do conceito de razão em densidade, massa específica, razão trigonométrica em uma situaçã;o para na criação novo produto para o mercado envolvendo um novo material.
Na vida profissional os conceitos da matemática jamais aparece isoladamente. Cada situação real envolve vários conceitos e conteúdos e que, é o engenheito precisa fazer um modelo matemático para uma situação totalmente nova. Clique sobre a imagem.Problemas resolvidos que envolvem razão entre grandezas
2.1.2 Proporção
2.1.2.1 Proporção como igualdade de duas razões.
2.1.2.2 Propriedades das proporções
Assista os vídeos dos endereços a seguir:
https://www.youtube.com/watch?v=0AzClo5G9KM;
https://www.youtube.com/watch?v=sD_vgL4HHPQ;
2.1.2.3 Relação de proporcionalidade
Diz-se que existe uma relação de proporcionalidade entre duas variáveis reais x e y não nulas, se e somente se y=kx ou y =k/x, onde k deve permanecer constante para todo x e y.
Quando y=kx, então x e y são diretamente proporcionais.
Quando y=k/x , então x e y são inversamente proporcionais.2.1.2.3.1 Relação de proporcionalidade: y=kx(grandezas diretamente proporcionais)
Veja exemplo na imagem a seguir
Relação de proporcionalidade na composição da gasolina comum
Vamos encontrar a função que representa a relação entre o volume de etanol anidro(y) a ser adicionada à gasolina tipo A(x) para formar a gasolina comum (x+y).
Em abril de 2019, na composição gasolina comum, 27% deve ser etanol e o restante (73%) deve ser gasolina tipo A.
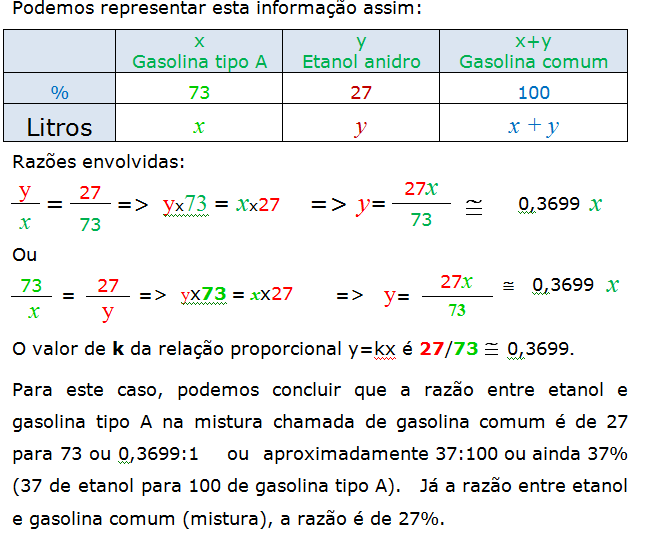
A função y=0,3699x pode ser utilizada para saber quanto de álcool deve ser adicionado à gasolina tipo A para que o porcentual de etanol presente na gasolina comum seja de 27%.
De modo similar podemos utilizar este esquema para fazer modelos matemáticos para outros casos de misturas que são feitas em fábricas que produzem os materiais para fabricar os produtos que vendem. Por exemplo: Numa fábrica de tubos de concreto, os componentes da mistura utilizada, mantém relações de proporcionalidade entre si, para que as propriedades do material produzido se mantenha constante.A primeira Lei de OHM é também um exemplo de grandezas diretamente proporcionais.
Fonte da imagem: <http://www.diaadiaeducacao.pr.gov.br> Acesso em mar. 2019.
2.1.2.3.2 Relação de proporcionalidade inversa: y=k/x para Grandezas inversamente proporcionais
Exemplo.
O valor de k da relação inversamente proporcional y=k/x é 84,95x 0,2 = 16,99.
A função y=16,99/x pode ser utilizada para saber a resistência de fios feitos com o mesmo material, para o mesmo comprimento mas de diâmetros diferentes.A segunda Lei de OHM é também um exemplo de grandezas inversamente proporcionais.
Fonte da imagem: <http://www.diaadiaeducacao.pr.gov.br> Acesso em mar. 2019.2.2 Regra de Três
2.2.2.1 Situação para uso da regra de três para grandezas diretamente proporcional
Se as grandezas envolvidas são diretamente proporcionais, é utilizada a propriedade: a primeira razão é igual a segunda razão ou seja, a divisão dos valores dos termos y e x é sempre o mesmo (y/x = k ou ainda y=kx).
Veja a situação da imagem a seguir.

Fonte da imagem:
<http://www.projetos.unijui.edu.br/matematica/estatistica/Objeto4/index.html&rt;
2.2.2.2 Situação para uso da regra de três para grandezas inversamente proporcionais
Se as grandezas envolvidas são inversamente proporcionais, é utilizada a propriedade: “a primeira razão é igual a segunda razão invertida, ou seja, o produto dos valores dos termos y e x é sempre o mesmo (x.y = k ou ainda y=k/x).
Veja a situação a seguir.

Resolva os exercícios do endereço a seguir:
https://pt.khanacademy.org/math/pre-algebra Inscreva-se neste canal para rever conceitos básicos da matemática elementar.2.3 Porcentagem
A porcentagem é uma razão onde o segundo termo é 100 ou uma fração com denominador 100. Ao invés de colocar o número 100 no segundo termo da razão ou no denominador, coloca-se o símbolo%. Este símbolo sempre indica divisão por 100.
Taxas de juros muitas vezes são expressas em taxa unitário, ou seja, expressa uma razão cujo segundo termo é 1, neste caso as taxas estão escritas em decimais. Se multiplicar a taxa unitária por 100 e acrescentar o símbolo de % já estará transformada para porcentagem.
Para resolver problemas de porcentagem pode-se utilizar a regra de três, ou seja, pela entre duas razões.A seguir são apresentadas situações que envolvem porcentagem. Resolva cada situação problema apresentada o item a seguir.
2.3.1 Problemas que envolvem porcentagem
Segue uma lista de problemas corriqueiros que podem ser resolvidos utilizando a propriedade fundamental das proporções.
Para sumular vários tipos de problemas que envovem os conteúdos da unidade 2 e início da unidade 3, baixe a planilha a seguir.